Les arbres de décision¶

Un arbre de décision est une structure de branchement binaire utilisée pour classer un vecteur d’entrée arbitraire $X$. Chaque nœud de l’arbre contient une simple comparaison de caractéristiques par rapport à un champ $x_{i} \in X,$ comme “est-ce que $x_{i} \geq 35 ? "$ le résultat de chacune de ces comparaisons est soit vrai, soit faux, ce qui détermine si nous devons passer à la branche gauche ou droite du nœud donné.

Sur le plan terminologique, les termes suivants sont utiles pour décrire un arbre décisionnel général :

Nœud racine (Root node): Il s’agit du nœud situé au sommet d’un arbre décisionnel représentant l’ensemble des données. Dans la figure 8.1 .1 (a), le nœud racine se trouve juste avant la première division par $X_{1}<10$.
Nœuds terminaux (ou feuilles ou Terminal nodes) : Il s’agit de nœuds qui ne sont plus divisés et qui constituent une fin en soi ($R_2=\left( \mathbf{Y} | \mathbf{X_2} > 4.5 \ ,\mathbf{X_1} \leq 117.5 \right) =402 \ 783 \ \$ $)
Nœuds internes : Il s’agit des points de l’arbre où l’espace des prédicteurs est divisé.
Branches : Ce sont des lignes reliant différents nœuds (terminaux ou internes).

Ces structures sont parfois appelées arbres de classification et de régression (classification and regression trees - CART), car elles peuvent être appliquées aux deux sortes de problèmes.

Les avantages des arbres de décision sont les suivants:

Non-linéarité : Chaque feuille représente une partie de l’espace de décision, mais on y accède par un chemin potentiellement compliqué. Cette chaîne logique permet aux arbres de décision de représenter des limites de décision très complexes.
Prise en charge des variables catégorielles : Les arbres de décision utilisent naturellement des variables catégorielles, comme “si la couleur des cheveux = rouge”, en plus des données numériques. Les variables catégorielles s’adaptent moins bien à la plupart des autres méthodes d’apprentissage automatique.
Interprétabilité : Les arbres de décision sont explicables ; vous pouvez les lire et comprendre leur raisonnement. Ainsi, les algorithmes d’arbres de décision peuvent vous révéler quelque chose sur votre ensemble de données que vous n’auriez peut-être pas vu auparavant. En outre, l’interprétabilité vous permet de vérifier si vous avez confiance dans les décisions qu’il prendra : prend-il des décisions pour les bonnes raisons ?
Robustesse : Le nombre d’arbres de décision possibles croît de manière exponentielle avec le nombre de caractéristiques et de tests possibles, ce qui signifie que nous pouvons en construire autant que nous le souhaitons. Construire de nombreux arbres de décision aléatoires (CART) et considérer le résultat de chacun comme un vote pour l’étiquette donnée augmente la robustesse et nous permet d’évaluer la confiance de notre classification.
Application à la régression : Le sous-ensemble d’éléments qui suivent un chemin similaire dans un arbre de décision sont probablement similaires dans des propriétés autres que la seule étiquette. Pour chacun de ces sous-ensembles, nous pouvons utiliser la régression linéaire pour construire un modèle de prédiction spécial pour les valeurs numériques de ces éléments de la feuille. Ce modèle sera vraisemblablement plus performant qu’un modèle plus général entraîné sur toutes les instances.

Le plus grand inconvénient des arbres de décision est un certain manque d’élégance. Les méthodes d’apprentissage comme la régression logistique et les SVM font appel aux mathématiques. Théorie avancée des probabilités, algèbre linéaire, géométrie à haute dimension…etc.

En revanche, les arbres de décision sont un jeu de hacker. Il y a beaucoup de boutons à tourner dans la procédure de formation, et relativement peu de théorie pour vous aider à les tourner dans le bon sens.

Mais le fait est que les modèles d’arbres de décision fonctionnent très bien dans la pratique. Les arbres de décision par renforcements (GBDT) ont longtemps été (ils le sont de moins en moins) la méthode d’apprentissage machine la plus fréquemment utilisée pour remporter les compétitions Kaggle.

Exemple introductif¶

Pour mieux comprendre l’idée derrière les arbres de régression, reprenons un exemple simple qui a été illustré dans le livre [JWHT13]. Dans cet exemple, les auteurs tentent de prédire le salaire d’un joueur de baseball ($\mathbf{Y}$ variable réponse) en se basant sur deux variables explicatives, soient le nombre de points produits $\mathbf{X_1}$ et l’expérience au sein de la ligue de baseball $\mathbf{X_2}$ exprimée en nombre d’années jouées.

Afin de visualiser les données de ce problème, nous allons utiliser un graphique en deux dimensions dans un système de coordonnées cartésiennes, où l’axe des ordonnées représente la première variable explicative $\mathbf{X_1}$ (le nombre de points produits par un joueur donné) et l’axe d’abscisses représente le nombre d’années jouées $\mathbf{X_2}$.

import matplotlib.style as style 
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
from sklearn import tree
import pandas as pd

df_hitters = pd.read_csv('https://raw.githubusercontent.com/nmeraihi/data/master/islr/Hitters.csv', index_col=0).dropna()
df_hitters.index.name = 'Player'
df_hitters.index = df_hitters.index.map(lambda x: x.replace('-', '', 1))
df_hitters["League"] = df_hitters["League"].astype('category')
df_hitters["Division"] = df_hitters["Division"].astype('category')
df_hitters["NewLeague"] = df_hitters["NewLeague"].astype('category')
df_hitters.head(3)

	AtBat	Hits	HmRun	Runs	RBI	Walks	Years	CAtBat	CHits	CHmRun	CRuns	CRBI	CWalks	League	Division	PutOuts	Assists	Errors	Salary	NewLeague
Player
Alan Ashby	315	81	7	24	38	39	14	3449	835	69	321	414	375	N	W	632	43	10	475.0	N
Alvin Davis	479	130	18	66	72	76	3	1624	457	63	224	266	263	A	W	880	82	14	480.0	A
Andre Dawson	496	141	20	65	78	37	11	5628	1575	225	828	838	354	N	E	200	11	3	500.0	N

df=df_hitters
df["log_sal"]=np.log(df.Salary.values)

style.use('ggplot')
sns.set_context('paper')
plt.style.use('seaborn-darkgrid');

ax=sns.lmplot(x='Years', 
           y='Hits', 
           data=df, 
           fit_reg=False, 
           hue="log_sal",
           legend=False, 
           palette="BuPu", height=4, aspect=11.7/8.27)
ax.set(xlabel='Expérience en années', ylabel='Points produits')
plt.show()

ax2=sns.distplot(df.Salary, kde=False, rug=True);
ax2.set(xlabel='Salaire en milliers de dollars', ylabel='Fréquence')
plt.show()

Dans les deux figures précédentes, les salaires sont présentés par des points ayant comme coordonnées les deux variables explicatives. Nous pouvons voir la variable réponse comme une troisième dimension reliant les points produits par un joueur donné et son expérience. Ces points seront plus foncés pour les salaires les plus élevés et plus clairs pour les salaires les plus faibles.

Nous pouvons constater, que les joueurs les mieux payés sont ceux ayant le plus d’expérience et ayant produit le plus de points, donc les points situés sur le quart supérieur droit, à l’exception des deux points situés au coin inférieur gauche. Ces derniers peuvent être vus comme de jeunes joueurs considérés comme de futures vedettes.

Sur la première figure, nous séparons les points en trois groupes, de sorte à créer trois groupes de joueurs. Nous pouvons dès lors tracer une ligne verticale entre le point $\mathbf{X_2}=4$ et $\mathbf{X_2}=5$. Ainsi, nous avons deux groupes; des joueurs ayant plus que 4 années d’expérience et les autres ayant moins que 5 années d’expérience.

Nous pouvons ensuite clairement séparer le premier groupe en deux sous-groupes; des joueurs qui ont produit plus que 117 points ($\mathbf{X_1}>117$) et qui ont plus d’années d’expérience ($\mathbf{X_1}>4.5$), et le deuxième groupe qui est composé des joueurs ayant un nombre de points produits inférieurs à 118 points ($\mathbf{X_1}<118$) et qui ont eux aussi plus que 4.5 années d’expérience ($\mathbf{X_2}>4.5$). La segmentation que nous venons de faire est illustrée à la figure ci-dessous:

ax=sns.lmplot(x='Years', 
           y='Hits', 
           data=df, 
           fit_reg=False, 
           hue="log_sal",
           legend=False, 
           palette="BuPu", height=4, aspect=11.7/8.27)
plt.ylabel('Hits')
plt.xlabel('Years')
plt.xticks([1, 4.5, 24])
plt.yticks([1, 117.5, 238])
plt.vlines(4.5, ymin=-5, ymax=250)
plt.hlines(117.5, xmin=4.5, xmax=25)
plt.annotate('R1', color='purple',xy=(2,117.5), fontsize='xx-large')
plt.annotate('R2', color='purple',xy=(11,60), fontsize='xx-large')
plt.annotate('R3', color='purple',xy=(11,170), fontsize='xx-large')
plt.show()

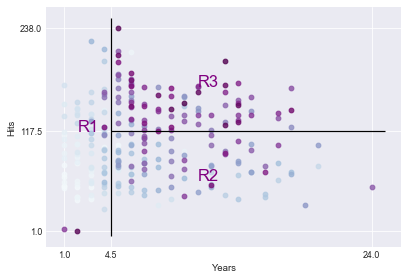
La séparation des points sur la figure ci-dessus que nous venons d’effectuer n’est rien d’autre qu’un arbre de décision. Nous pouvons remarquer sur cette même figure que nous avons trois niveaux (feuilles). Les joueurs ayant moins que 4.5 années d’expérience et ceux qui ont en plus. Ensuite, ce dernier groupe se divise en deux sous-groupes ; ceux qui ont produit moins que 118 buts et les joueurs ayant produit plus que 118.

Prédiction via la stratification de l’espace des caractéristiques¶

Nous allons maintenant aborder le processus de construction d’un arbre de régression. En gros, il y a deux étapes.

Nous divisons l’espace du prédicteur - c’est-à-dire l’ensemble des valeurs possibles pour $X_{1}, X_{2}, \ldots, X_{p}$ - en $J$ régions distinctes et non chevauchantes, $R_{1}, R_{2}, \ldots, R_{J}$.
Pour chaque observation qui tombe dans la région $R_{j},$ nous faisons la même prédiction, qui est simplement la moyenne des valeurs de réponse pour les observations d’apprentissage dans $R_{j}$.

Les régions $R_1, R_2, \dots , R_J$ peuvent avoir n’importe quelle forme géométrique. Toutefois, il a été choisi de diviser ces régions sous forme rectangulaire de deux dimensions dans l’exemple présenté précédemment. Dans un problème de classification, le but est de trouver les régions $R_1, R_2, \dots , R_J$ qui minimise la somme des carrés des résidus donnés par:

(9)¶\[\begin{equation} RSS=\sum_{j=1}^J \sum_{i \in R_j} \left(\mathbf{y_i} - \hat{\mathbf{y}}_{R_j} \right)^2 \end{equation}\]

où $\hat{\mathbf{y}}_{R_j}$ est la moyenne des valeurs de la variable réponse des données dans la $i$ème région.

Malheureusement, il n’est pas possible, d’un point de vue informatique, de considérer toutes les partitions possibles de l’espace des caractéristiques en J cases. L’approche est descendante parce qu’elle commence au sommet de l’arbre (à ce stade, toutes les observations appartiennent à une seule région) et divise ensuite successivement l’espace prédicteur ; chaque division est indiquée par deux nouvelles branches plus bas dans l’arbre. Il est gourmand parce qu’à chaque étape du processus de construction de l’arbre, la meilleure division est effectuée à cette étape particulière, plutôt que de regarder en avant et de choisir une division qui conduira à un meilleur arbre dans une étape future.

Afin d’effectuer une division binaire récursive, nous sélectionnons d’abord le prédicteur $X_{j}$ et le point de découpage $s$ de sorte que la division de l’espace des prédicteurs en régions $\left\{X \mid X_{j}<s\right\}$ et $\left\{X \mid X_{j} \geq s\right\}$ conduit à la plus grande réduction possible du RSS. (La notation $\left\{X \mid X_{j}<s\right\}$ désigne la région de l’espace des prédicteurs dans laquelle $X_{j}$ prend une valeur inférieure à s.) Autrement dit, nous considérons tous les prédicteurs $X_{1}, \ldots, X_{p},$ et toutes les valeurs possibles du point de coupure $s$ pour chacun des prédicteurs, puis nous choisissons le prédicteur et le point de coupure tels que l’arbre résultant présente le RSS le plus faible. De manière plus détaillée, pour tout $j$ et $s,$ nous définissons la paire de demi-plans suivants

\[R_{1}(j, s)=\left\{X \mid X_{j}<s\right\}$ and $R_{2}(j, s)=\left\{X \mid X_{j} \geq s\right\}\]

et nous cherchons la valeur de $j$ et $s$ qui minimise l’équation $$ \sum_{i: x_{i} \in R_{1}(j, s)}\left(y_{i}-\hat{y}_{R_{1}}\right)^{2}+\sum_{i: x_{i} \in R_{2}(j, s)}\left(y_{i}-\hat{y}_{R_{2}}\right)^{2} $$

où $\hat{y}_{R_{1}}$ est la réponse moyenne pour les observations d’apprentissage dans $R_{1}(j, s)$, et $\hat{y}_{R_{2}}$ est la réponse moyenne pour les observations d’apprentissage dans $R_{2}(j, s)$. La recherche des valeurs de $j$ et $s$ qui minimisent l’équation précédente peut être effectuée assez rapidement, en particulier lorsque le nombre de caractéristiques $p$ n’est pas trop grand.

Ensuite, nous répétons le processus, en recherchant le meilleur prédicteur et le meilleur point de coupure afin de diviser davantage les données de manière à minimiser le RSS dans chacune des régions résultantes. Cependant, cette fois-ci, au lieu de diviser l’espace prédicteur entier, nous divisons l’une des deux régions identifiées précédemment. Nous avons maintenant trois régions. De nouveau, nous cherchons à diviser davantage l’une de ces trois régions, de manière à minimiser le RSS. Le processus se poursuit jusqu’à ce qu’un critère d’arrêt soit atteint ; par exemple, nous pouvons continuer jusqu’à ce qu’aucune région ne contienne plus de cinq observations.

Une fois que les régions $R_{1}, \dots, R_{J}$ ont été créées, nous prédisons la réponse pour une observation test donnée en utilisant la moyenne des observations d’apprentissage dans la région à laquelle cette observation test appartient.

Élagage de l’arbre¶

Le processus décrit ci-dessus peut produire de bonnes prédictions sur l’ensemble d’apprentissage, mais il est probable qu’il surajuste les données, ce qui entraîne de mauvaises performances sur l’ensemble de test. Cela est dû au fait que l’arbre résultant peut être trop complexe. Un arbre plus petit avec moins de divisions (c’est-à-dire moins de régions $R_{1}, \dots, R_{J}$) pourrait conduire à une variance plus faible et à une meilleure interprétation au prix d’un léger biais. Une alternative possible au processus décrit ci-dessus consiste à ne construire l’arbre que tant que la diminution du RSS due à chaque division dépasse un certain seuil (élevé). Cette stratégie permet d’obtenir des arbres plus petits, mais elle est trop imprévoyante, car une division apparemment sans valeur au début de l’arbre peut être suivie d’une très bonne division, c’est-à-dire d’une division qui entraîne une forte réduction du RSS par la suite.

Par conséquent, une meilleure stratégie consiste à faire croître un très grand arbre $T_{0}$, puis à l’élaguer afin d’obtenir un sous-arbre. Comment déterminer la meilleure façon d’élaguer l’arbre ? Intuitivement, notre objectif est de sélectionner un sous-arbre qui conduit au taux d’erreur de test le plus faible. Étant donné un sous-arbre, nous pouvons estimer son erreur de test en utilisant la validation croisée ou l’approche de l’ensemble de validation. Cependant, l’estimation de l’erreur de validation croisée pour chaque sous-arbre possible serait trop lourde, car il existe un nombre extrêmement élevé de sous-arbres possibles. Au lieu de cela, nous avons besoin d’un moyen de sélectionner un petit ensemble de sous-arbres à prendre en compte.

Cost complexity pruning : Plutôt que de considérer tous les sous-arbres possibles, nous considérons une séquence d’arbres indexés par un paramètre d’ajustement non négatif $\alpha$.

\[\overbrace{\sum_{m=1}^{|T|} \underbrace{\sum_{i: \mathbf{x}_{i} \in R_{m}}\left(y_{i}-\hat{y}_{R_{m}}\right)^{2}}_{\text {RSS dans chaque noeud terminal}}}^{\text {somme sur tous les noeuds terminaux }}+\underbrace{\alpha|T|}_{\text {Cost complexity}},\]

\où :

$|T|$ désigne le nombre de noeud terminaux de l’arbre de décision en question.
est la réponse moyenne des observations d’apprentissage dans le millionième noeud terminal de l’arbre.
$\alpha$ est un paramètre d’ajustement non négatif. Pour chaque valeur de $\alpha,$ nous pouvons trouver un sous-arbre $T_{\alpha}\left(\right.$ of $\left.T_{0}\right),$ informellement écrit comme $T_{\alpha} \subset T_{0}$, qui minimise l’équation ci-dessus. On obtient alors une séquence de sous-arbres $\left\{T_{\alpha}\right\}$ de différents degrés de complexité indexés par $\alpha$.

Si l’on se souvient de ce que nous avons vu appris dans la section de régularisation rappelle fortement les motivations des méthodes de régularisation et implique la même formulation “perte + pénalité”. Si $\alpha=0,$ alors il n’y a pas de prix à payer pour rendre l’arbre complexe et la solution est identique au grand arbre $T_{0}$. Lorsque $\alpha$ augmente, le terme de pénalité devient plus important et la croissance d’un grand arbre est de plus en plus sévèrement punie, de sorte que $T_{\alpha}$ diminue en taille (avec moins de nœuds terminaux). Un attrait particulier de l’élagage de la complexité des coûts est qu’il produit une famille d’arbres imbriqués : Si ${\alpha_{1}} \leq \alpha_{2}$, alors $T_{\alpha_{2}}$ (le plus petit arbre) est imbriqué dans $T_{\alpha_{1}}$ (le plus grand arbre) dans le sens où tous les nœuds de $T_{\alpha_{2}}$ forment un sous-ensemble des nœuds de $T_{\alpha_{1}}$. Nous pouvons donc faire varier manuellement $\alpha$ en fonction du niveau de complexité de l’arbre souhaité ou, mieux encore, utiliser la validation croisée pour sélectionner $\alpha$ (c’est-à-dire produire une grille de valeurs de $\alpha$ et choisir celle qui entraîne la plus petite erreur de validation croisée).

Classification¶

Les arbres de classification fonctionnent à peu près de la même manière que les arbres de régression, à l’exception du calcul de la prédiction ainsi que le calcul de l’érreur de classification (au lieu de la régression). Dans le premier cas, nous calculons le mode au lieu de la moyenne. Dans le deuxième cas, nous calculons le taux d’érreur de lcassification qui est simplement la fraction des observations d’entraînement dans cette région qui n’appartiennent pas à la classe la plus commune :

\[E=1-\max _{k}\left(\hat{p}_{m k}\right)\]

Ici, $\hat{p}_{m k}$ représente la proportion d’observations des données d’entraînement dans la région $m$ qui appartiennent à la classe $k$.

En effet, $\max _{k}\left(\hat{p}_{m k}\right)$ donne la proportion d’observations dans $R_{m}$ qui appartiennent à la classe la plus fréquente et $1-\max _{k}\left(\hat{p}_{m k}\right)$ donne la proportion d’observations qui ne le sont pas et donc mal classées. Dans le cas particulier de $K=2$, la classe prédite est la classe pour laquelle la proportion d’observations de l’échantillon est supérieure à 0,5 .

Cependant, il s’avère que l’erreur de classification n’est pas suffisamment sensible pour l’arborescence, et en pratique, deux autres mesures sont préférables.

Gini index¶

\[G=\sum_{k=1}^{K} \hat{p}_{m k}\left(1-\hat{p}_{m k}\right)\]

qui est une mesure de la variance entre les $K$ classes de la réponse qualitative. Plus le degré de pureté de $R_{m}$ est élevé, plus la valeur de l’indice de Gini est faible. En effet, nous pouvons écrire l’indice de Gini comme suit

\[G_{m}=\sum_{k=1}^{K} \hat{p}_{m k}-\sum_{k=1}^{K} \hat{p}_{m k}^{2}=1-\sum_{k=1}^{K} \hat{p}_{m k}^{2}\]

qui atteint sa valeur minimale de zéro si $\hat{p}_{m k}=1$ pour un certain $k$ (les observations sont toutes concentrées sur une classe) et sa valeur maximale si $\hat{p}_{m 1}=\cdots=\hat{p}_{m K}=1 / K$ (les observations sont uniformément réparties entre les $K$ classes). Dans le cas particulier de $K=2$, l’indice de Gini se simplifie en

\[G_{m}= 2 \hat{p}_{m 1}\left(1-\hat{p}_{m 1}\right)\]

Exemple;¶

À un nœud particulier de l’arbre, 73 observations ont une valeur “oui” et 27 observations ont une valeur “Non”. Calculez l’indice de Gini de ce noeud

oui=73
non=27
probOui=oui/(oui+non)
probNon=1-probOui

2*(probOui)*(1-probOui)

0.3942

cross-entropy¶

Une alternative à l’indice de Gini est l’entropie croisée, donnée par:

\[D=-\sum_{k=1}^{K} \hat{p}_{m k} \log \hat{p}_{m k}\]

-(probOui *np.log(probOui) + probNon*np.log(probNon))

0.583258840128597

Regardons plus en détail ce que cela donne sur les données iris

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier

iris = load_iris()
X = iris.data[:, 2:] 
y = iris.target

tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_clf.fit(X, y)

DecisionTreeClassifier(ccp_alpha=0.0, class_weight=None, criterion='gini',
                       max_depth=2, max_features=None, max_leaf_nodes=None,
                       min_impurity_decrease=0.0, min_impurity_split=None,
                       min_samples_leaf=1, min_samples_split=2,
                       min_weight_fraction_leaf=0.0, presort='deprecated',
                       random_state=42, splitter='best')

plt.style.use('classic')
fig = plt.figure(figsize=(12.5,10))
_ = tree.plot_tree(tree_clf, feature_names=iris.feature_names[2:],class_names=iris.target_names, filled=True)

text_representation = tree.export_text(tree_clf)
print(text_representation)

|--- feature_0 <= 2.45
|   |--- class: 0
|--- feature_0 >  2.45
|   |--- feature_1 <= 1.75
|   |   |--- class: 1
|   |--- feature_1 >  1.75
|   |   |--- class: 2

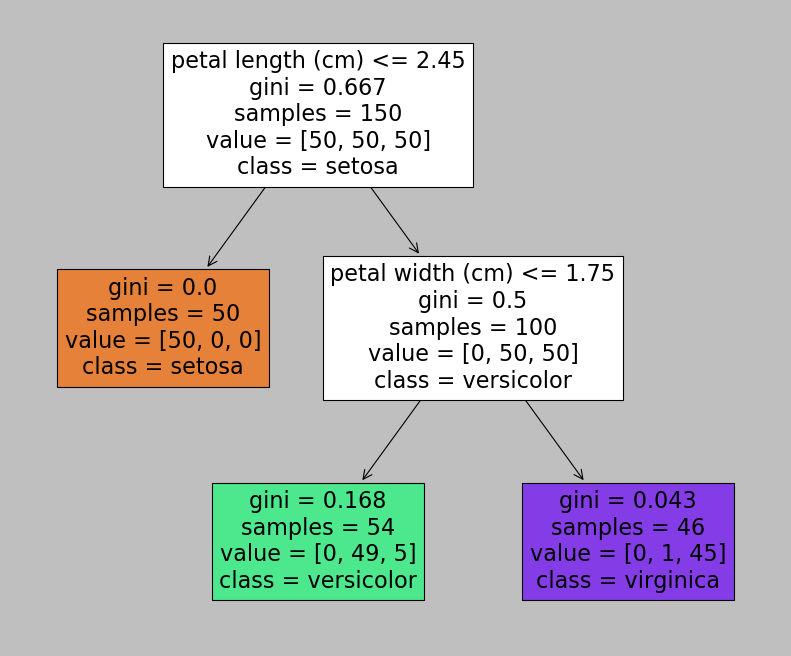
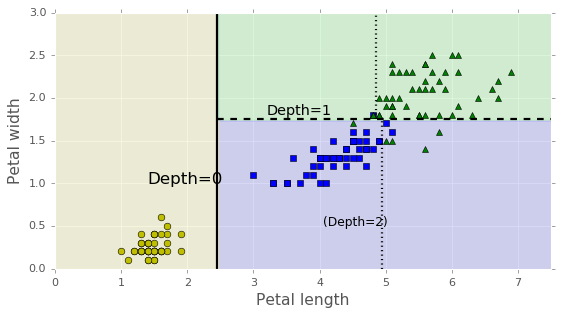
Un arbre de décision peut également estimer la probabilité d’appartenance d’une instance à une classe particulière k : il parcourt d’abord l’arbre pour trouver le nœud de la feuille correspondant à cette instance, puis il renvoie le rapport des instances d’apprentissage de la classe k dans ce nœud. Par exemple, supposons que vous ayez trouvé une fleur dont les pétales mesurent 5 cm de long et 1,5 cm de large. Le nœud de feuille correspondant est le nœud gauche de profondeur 2, et l’arbre de décision devrait donc produire les probabilités suivantes : 0% pour Iris-Setosa (0/54), 90,7% pour Iris-Versicolor (49/54) et 9,3% pour Iris-Virginica (5/54). Et bien sûr, si vous lui demandez de prédire la classe, il devrait sortir Iris-Versicolor (classe 1) puisqu’elle a la plus grande probabilité. Vérifions cela :

tree_clf.predict_proba([[5, 1.5]])

array([[0.        , 0.90740741, 0.09259259]])

Instabilité¶

On a vu que les arbres de décision ont beaucoup d’atouts : ils sont simples à comprendre et à interpréter, faciles à utiliser, polyvalents et assez puissants. Cependant, ils présentent quelques limites. Tout d’abord, comme on l’a déjà remarqué, les arbres de décision fonctionnent bien lorsqu’on a les séparations de décision orthogonales (tous les fractionnements sont perpendiculaires à un axe), ce qui les rend sensibles à la rotation de l’ensemble d’apprentissage.

Plus généralement, le principal problème des arbres de décision est qu’ils sont très sensibles aux petites variations des données d’entrainement. Par exemple, si vous supprimez simplement l’Iris- Versicolor le plus large de l’ensemble de données d’iris (celui dont les pétales mesurent 4,8 cm de long et 1,8 cm de large) et qu’on ajuste un nouvel arbre de décision, on obtient le modèle représenté à la figure ci-dessous. Comme vous pouvez le constater, il est très différent de l’arbre de décision précédent précédent.

X[(X[:, 1]==X[:, 1][y==1].max()) & (y==1)]

array([[4.8, 1.8]])

not_widest_versicolor = (X[:, 1]!=1.8) | (y==2)
X_tweaked = X[not_widest_versicolor]
y_tweaked = y[not_widest_versicolor]

tree_clf_tweaked = DecisionTreeClassifier(max_depth=2, random_state=40)
tree_clf_tweaked.fit(X_tweaked, y_tweaked)

DecisionTreeClassifier(ccp_alpha=0.0, class_weight=None, criterion='gini',
                       max_depth=2, max_features=None, max_leaf_nodes=None,
                       min_impurity_decrease=0.0, min_impurity_split=None,
                       min_samples_leaf=1, min_samples_split=2,
                       min_weight_fraction_leaf=0.0, presort='deprecated',
                       random_state=40, splitter='best')

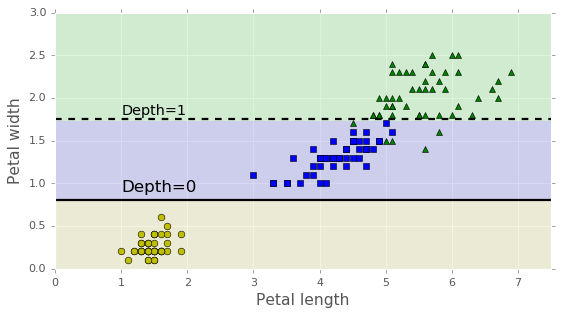
Nous veerons dans le prochain cours une technique qui corrige ces lacunes

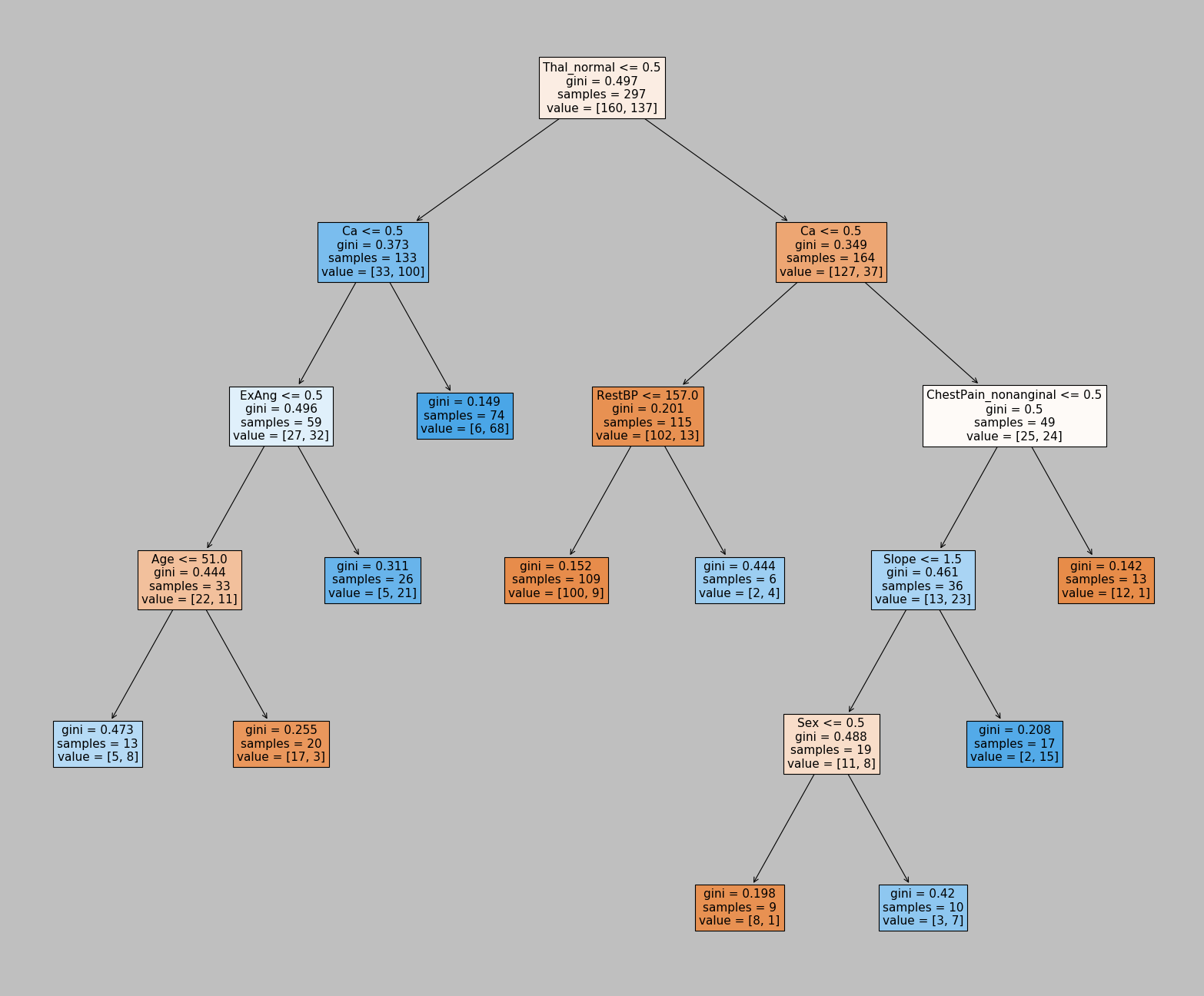
Exemple ISLR¶

Exemple de la page 312 du ISLR [JWHT13]

df_heart = pd.read_csv('https://raw.githubusercontent.com/nmeraihi/data/master/islr/Heart.csv', index_col=0).dropna()
for cat_col in ['ChestPain', 'Thal', 'AHD']:
    df_heart[cat_col] = df_heart[cat_col].astype('category')
    print(f'{cat_col}: {df_heart[cat_col].cat.categories.values}')

ChestPain: ['asymptomatic' 'nonanginal' 'nontypical' 'typical']
Thal: ['fixed' 'normal' 'reversable']
AHD: ['No' 'Yes']

df_heart.head(3)

	Age	Sex	ChestPain	RestBP	Chol	Fbs	RestECG	MaxHR	ExAng	Oldpeak	Slope	Ca	Thal	AHD
1	63	1	typical	145	233	1	2	150	0	2.3	3	0.0	fixed	No
2	67	1	asymptomatic	160	286	0	2	108	1	1.5	2	3.0	normal	Yes
3	67	1	asymptomatic	120	229	0	2	129	1	2.6	2	2.0	reversable	Yes

X = pd.get_dummies(df_heart[df_heart.columns.difference(['AHD'])], drop_first=True)
y = pd.get_dummies(df_heart.AHD, drop_first=True)

from sklearn.tree import DecisionTreeClassifier

clf = DecisionTreeClassifier(max_depth=6, min_impurity_decrease=0.01)
clf.fit(X, y)

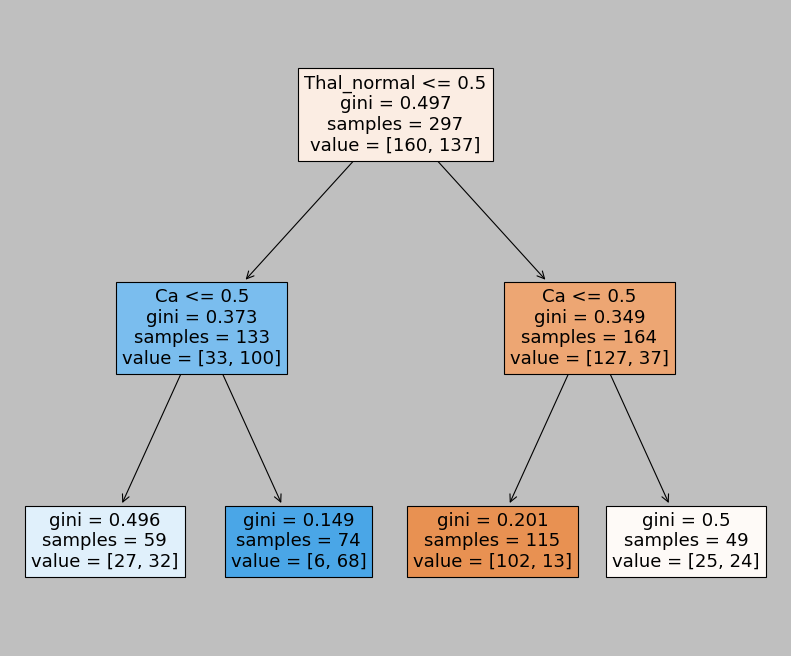
DecisionTreeClassifier(ccp_alpha=0.0, class_weight=None, criterion='gini',
                       max_depth=6, max_features=None, max_leaf_nodes=None,
                       min_impurity_decrease=0.01, min_impurity_split=None,
                       min_samples_leaf=1, min_samples_split=2,
                       min_weight_fraction_leaf=0.0, presort='deprecated',
                       random_state=None, splitter='best')

plt.style.use('classic')
fig = plt.figure(figsize=(25,20))
_ = tree.plot_tree(clf, feature_names=X.columns, filled=True)

from sklearn.model_selection import train_test_split, cross_val_score

scores = []
max_leafs_arr = range(2, 50)
for max_leafs in max_leafs_arr:
    regressionTree = DecisionTreeClassifier(max_leaf_nodes=max_leafs)
    sc = cross_val_score(regressionTree, X, y, cv=10)
    scores.append((sc.mean(), sc.std()))
scores = np.array(scores)

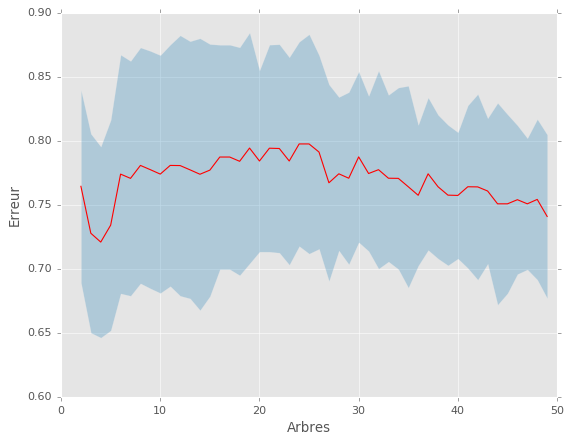
plt.plot(max_leafs_arr, scores[:,0], 'r')
plt.fill_between(max_leafs_arr, scores[:,0]+scores[:,1], scores[:,0]-scores[:,1], alpha=0.3)
plt.xlabel('Arbres')
plt.ylabel('Erreur')
plt.style.use('ggplot')
best_min_leafs = max_leafs_arr[np.argmin(scores[:,0])]
print(f"The best tree has {best_min_leafs} leafs.")

The best tree has 4 leafs.

plt.style.use('classic')
fig = plt.figure(figsize=(12.5,10))
_ = tree.plot_tree(DecisionTreeClassifier(max_leaf_nodes=best_min_leafs).fit(X,y), 
                   feature_names=X.columns,
                   filled=True)

Bibliographie¶

JWHT13(1,2): Gareth James, Daniela Witten, Trevor Hastie, and Robert Tibshirani. An introduction to statistical learning. Volume 112. Springer, 2013.

ACT6100