Réduction des dimensions¶

De nombreux problèmes d’apprentissage machine impliquent des milliers, voire des millions de variables explicatives pour chaque ensemble de données d’entraînement. Non seulement cela rend la phase d’entraînement du modèle extrêmement lente, mais cela peut aussi rendre beaucoup plus difficile la recherche d’une bonne solution.

Heureusenemnt, il existe des techniques de réduction de dimensions qui nous permettent de traiter ces données impliquant des millions de variables. Avant de plonger dans la réduction des dimensions, regardons quelques exemples de données dont l’aspect des dimensions est important.

Exemple des images¶

Il est souvent possible de réduire considérablement le nombre de variables explicatives. Prenons par exemple les images du MNIST [LBBH98] qui est un ensemble de 70 000 petites images de chiffres manuscrits par des collégiens et des employés du Bureau du recensement américain. Chaque image est étiquetée avec le chiffre qu’elle représente.

from tensorflow.keras.datasets import mnist
(X_train, Y_train), (X_test, Y_test) = mnist.load_data()

import matplotlib.pyplot as plt
%matplotlib inline

num = 10
images = X_train[:num]
labels = Y_train[:num]

num_row = 2
num_col = 5
fig, axes = plt.subplots(num_row, num_col, figsize=(1.5*num_col,2*num_row))
for i in range(10):
    ax = axes[i//num_col, i%num_col]
    ax.imshow(images[i], cmap='gray')
    ax.set_title('Label: {}'.format(labels[i]))
plt.tight_layout()
plt.show()

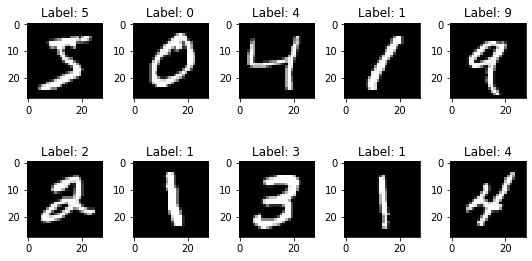
Les pixels de l’image sont presque toujours blancs (ou noir en contrast), ce qui permet de les supprimer complètement du jeu d’entraînement sans perdre beaucoup d’informations. Les pixels ne sont absolument pas importants pour la tâche de classification. De plus, deux pixels voisins sont souvent fortement corrélés : si vous les fusionnez en un seul pixel (par exemple en prenant la moyenne des intensités des deux pixels), vous ne perdrez pas beaucoup d’informations.

sample = 1
image = X_train[sample]# plot the sample
fig = plt.figure(figsize=(12, 7.6))
plt.imshow(image, cmap='gray_r')
plt.show()

Dans le cas des de classification des images, la réduction de la dimensionnalité fait perdre certaines informations, donc même si elle accélère la phase d’entraînement du modèle, elle peut aussi rendre votre modèle légèrement moins performant.

Cela rend également vos pipeline un peu plus complexes et donc plus difficiles à entretenir. Vous devez donc d’abord essayer d’entraîner votre modèle avec les données originales avant d’envisager d’utiliser la réduction de la dimensionnalité.

Très haute dimensions¶

Nous pouvons faire face des fois à des défis de “taille”, comme la taille des images de très hautes résolution. En effet, certains images nous sont des fois remis avec un très haute résolution. Dans l’exemple ci-dessous, nous avons l’image de l’herbacé Amarante réfléchie Amaranthus retroflexus;

Si l’on compare cette graine à celle de l’amarante épineuse (Amaranthus spinosus), on peut voir que ces deux se ressemblent énormément;

Dans d’autres cas, nous avons des images avec plusieurs couches afin de reprodit un effet 3D, cela rend encore les images extrêment en très haute résolution. Dans l’exemple ci-dessous, nous avons une résolution 5000x2000 pixels.

Or, appliquer une réduction de dimension dans de tels problèmes risque de réduire énormément le taux de justesse du modèle de classification.

Exemple d’imagerie spectrale¶

Certains détails dans les images RGB que nous appercevons avec notre oeil peuvent manquer beaucoup de détail. Par exemple [BMS+21] démontre l’importance et la haute performance de l’imagerie spectrale comme outil rapide et polyvalent pour évaluer les attributs de la germination des graines.

Dans un article récent [LFZ+20], un groupe de recherche chinois montre que trois variétés de graines de poivron peuvent être distinguées des images spectrales avec une précision de classification de plus de 97 %. Les classificateurs SVM, CNN et kNN ont été utilisés et comparés. Les tests de pureté génétique rapides et non destructifs ont un potentiel énorme dans l’industrie des semences et cet article montre l’importance de l’imagerie spectrale pour l’analyse des semences dans une autre culture importante.

La dimensionnalité¶

Pour nous (les humains), il est extrement difficile (voir impossible) d’imaginer un monde au delà de \(d>3\) dimensions. Habituellement, le mieux que nous puissions faire est de penser aux géométries à haute dimension par l’algèbre linéaire : les équations qui régissent notre compréhension des géométries à deux/trois dimensions se généralisent facilement pour un \(d\) arbitraire, et c’est ainsi que les choses fonctionnent.

Nous pouvons développer une certaine intuition sur comment travailler avec un ensemble de données à plus haute dimension par des méthodes de projection, qui réduisent la dimensionnalité à des niveaux que nous pouvons comprendre. Il est souvent utile de visualiser les projections bidimensionnelles des données en ignorant entièrement les autres dimensions \(d-2\), et d’étudier plutôt les tracés en points des paires de dimensions. Grâce à des méthodes de réduction des dimensions telles que l’analyse par composante principale (voir les prochaines sections), nous pouvons combiner des caractéristiques fortement corrélées pour produire une représentation plus nette. Bien entendu, certains détails sont perdus au cours du processus.

Il doit être clair qu’en augmentant le nombre de dimensions dans notre ensemble de données, nous disons implicitement que chaque dimension est une partie moins importante de l’ensemble. En mesurant la distance entre deux points dans l’espace des caractéristiques, comprenez qu’un grand \(d\) signifie qu’il y a plus de façons pour les points d’être proches (ou éloignés) les uns des autres : nous pouvons imaginer qu’ils sont presque identiques dans toutes les dimensions sauf une.

C’est pourquoi le choix de la mesure de la distance est le plus important dans les espaces de données à haute dimension. Bien sûr, nous pouvons toujours nous en tenir à la distance \(L_2\), qui est un choix sûr et standard. Mais si nous voulons récompenser les points pour être proches sur de nombreuses dimensions, nous préférons une métrique qui penche davantage vers \(L_1\). Si, au contraire, les choses sont similaires alors qu’il n’y a pas de champs uniques de dissimilitude flagrante, nous devrions peut-être nous intéresser à quelque chose de plus proche de \(L_{\infty}\).

Avant de nous plonger dans des algorithmes spécifiques de réduction de la dimensionnalité, examinons la principale approche de réduction de la dimensionnalité : la projection.

Projection¶

Dans la plupart des problèmes, les observations ne sont pas réparties uniformément dans toutes les dimensions. De nombreuses caractéristiques sont presque constantes, tandis que d’autres sont fortement corrélées. Par conséquent, toutes les instances d’entraînement se trouvent en fait dans (ou à proximité de) un sous-espace de dimension beaucoup plus bas de l’espace de haute dimension. Regardons un exemple où l’on peut voir un ensemble de données 3D représenté par les cercles.

Transformer le plan en fonction de \(x\) et \(y\).

pca = PCA(n_components = 2)
X2D = pca.fit_transform(X)

X3D_inv = pca.inverse_transform(X2D)

Tracez le jeu de données 3D, le plan et les projections sur ce plan.

print(pca.explained_variance_ratio_)

[0.84248607 0.14631839]

0.84248607 + 0.14631839

0.98880446

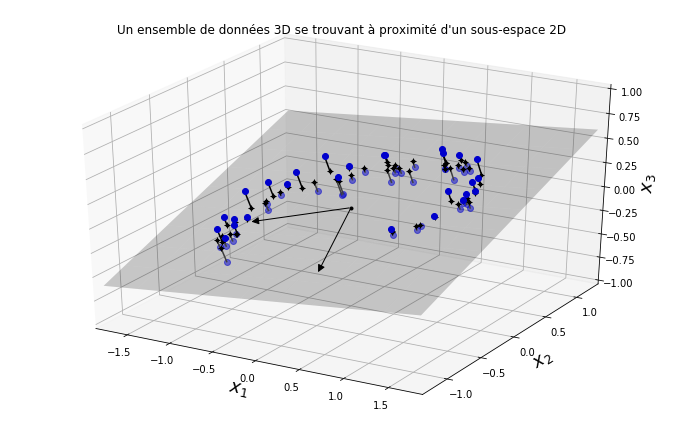
Si nous projetons chaque observation perpendiculairement à ce sous-espace (comme représenté par les lignes courtes reliant les observations de l’hyperplan), nous obtenons le nouvel ensemble de données 2D illustré à la figure ci-dessous.Nous venons de réduire la dimension de l’ensemble de données de 3D à 2D. Notez que les axes correspondent aux nouvelles variables \(z_{1}\) et \(z_{2}\) (les coordonnées des projections sur le plan).

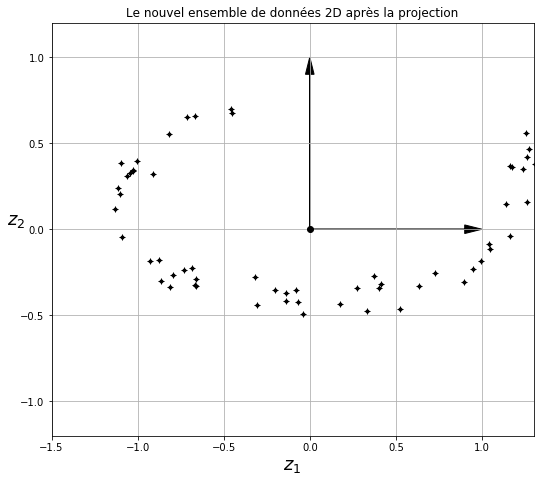
Cependant, la projection n’est pas toujours la meilleure approche pour réduire la dimensionnalité. Dans de nombreux cas, le sous-espace peut prendre différentes formes, comme dans le célèbre ensemble de données sur des jouets roulants suisses représenté dans la figure ci-dessous

Computing LLE embedding
Done. Reconstruction error: 1.1293e-07

Une simple projection sur un plan (par exemple, en laissant tomber l’axe \(z\)) écraserait différentes couches du rouleau suisse ensemble. Cependant, ce que vous voulez vraiment, c’est dérouler le rouleau suisse pour obtenir l’ensemble de données en 2D comme le montre la figure ci-dessous.

BMS+21: Vitor de Jesus Martins Bianchini, Gabriel Moura Mascarin, Lúcia Cristina Aparecida Santos Silva, Valter Arthur, Jens Michael Carstensen, Birte Boelt, and Clíssia Barboza da Silva. Multispectral and x-ray images for characterization of jatropha curcas l. seed quality. Plant Methods, 17(1):1–13, 2021.
LBBH98: Yann LeCun, Léon Bottou, Yoshua Bengio, and Patrick Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11):2278–2324, 1998.
LFZ+20: Xingwang Li, Xiaofei Fan, Lili Zhao, Sheng Huang, Yi He, and Xuesong Suo. Discrimination of pepper seed varieties by multispectral imaging combined with machine learning. Applied Engineering in Agriculture, 36(5):743–749, 2020.

ACT6100