Régression linéaire¶
Dans ce cours, nous traitons la régression linéaire, une approche très simple pour l’apprentissage supervisé. En particulier, la régression linéaire est un outil utile pour prédire une variable réponse quantitative.
Régression linéaire simple¶
La régression linéaire simple porte bien son nom : il s’agit d’une approche très simple pour prédire une réponse quantitative Y sur la base d’une variable prédictive X sin- gle. Elle suppose qu’il existe approximativement une relation linéaire entre X et Y . Mathématiquement, nous pouvons écrire cette relation linéaire comme
Dans l’équation (1) , β0 et β1 sont deux constantes inconnues qui représentent les termes de l’intercept (β0) et de la pente (β1 ) dans le modèle linéaire. Ils sont connus comme les coefficients ou paramètres du modèle.
Une fois que nous avons utilisé nos données d’entraînement du modèle pour estimer ˆβ0 et ˆβ1, nous pouvons prédire nos Y en écrivant:
Estimation des coefficients¶
Soit ˆy=ˆβ0+ˆβ1X la prédiction pour Y sur la ième valeur de X. Pour chaque point rouge dans la figure ci-dessous, on peut calculer “de combien on s’est trompé” dans note modèle, en calculant la distance (verticale) entre le point rouge et la droite bleue qui la régression linéaire simple de notre jeu de données.
Alors pour chaque point i, nous pouvons écrire ei=yi−ˆyi. Nous appelons ei le ième résidu. Nous pouvons calculer la somme du carré (valeur positives et négatives) des résidus par:
ou de manière équivalente à
Le but bien évidemment est d’avoir cette somme des résidus la plus petite possible. Nous devons donc minimiser RSS
L’approche des moindres carrés choisit β0 et β0 pour minimiser le RSS. On peut montrer que;
où ˉy=1n∑ni=1yi etˉx=1n∑ni=1xi sont les moyennes d’échantillonnage. En d’autres termes, (3.4.1) et (3.4.2) définissent les estimations des coefficients des moindres carrés pour la régression linéaire simple.
Soit le vecteur de paramètres β; $β:=[β0,…β1]T,$
le vecteur de la variable réponse des données d’entraînement:
et la matrice contenant les prédicteurs de l’ensemble des données d’entraînement:
Montrer que l’estimateur OLS ( ordinary least square ) des paramètres β dans une régression linéaire est donné par:
import numpy as np
import matplotlib.pyplot as plt
import scipy.linalg as la
from IPython.core.display import display, HTML
from plotly.offline import download_plotlyjs, init_notebook_mode, plot, iplot
Faisons un exemple avec quelques fausses données. Construisons un ensemble de points aléatoires en nous basant sur le modèle $y=β0+β1x+ϵ$
beta_0 = 2
beta_1 = 3
N = 100
x = np.random.rand(100)
noise = 0.1*np.random.randn(100)
y = beta_0 + beta_1*x + noise
Construisons la matrice X:
X = np.column_stack([np.ones(N),x])
print(X.shape)
(100, 2)
X[:5,:]
array([[1. , 0.09832457],
[1. , 0.79201449],
[1. , 0.53882094],
[1. , 0.10450947],
[1. , 0.28303924]])
beta_hat = la.solve(X.T @ X, X.T @ y)
print(beta_hat)
[2.00749293 2.96924115]
Exemple 3.1.1¶
Voici l’exemple de la section 3.1.1 du cite{james2013introduction}
import pandas as pd
import numpy as np
advertising = pd.read_csv('https://raw.githubusercontent.com/nmeraihi/data/master/islr/Advertising.csv', usecols=[1,2,3,4])
from sklearn.preprocessing import scale
import sklearn.linear_model as skl_lm
regr = skl_lm.LinearRegression()
X = advertising.TV.values.reshape(-1,1)
y = advertising.Sales
regr.fit(X,y)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
Estimation des Coefficients avec Sklearn¶
regression=regr.predict(X)
print("beta0=", regr.intercept_, "beta1=", regr.coef_)
beta0= 7.032593549127693 beta1= [0.04753664]
Estimation des Coefficients avec statsmodels¶
import statsmodels.formula.api as smf
model1=smf.ols(formula='Sales~TV',data=advertising).fit()
model1.params
Intercept 7.032594
TV 0.047537
dtype: float64
On peut donc écrire:
L’équation ci-dessus implique donc qu’une augmentation de 100 unités des coûts de publicité (TV) augmentera les vente de quatre unités.
model1.summary()
| Dep. Variable: | Sales | R-squared: | 0.612 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.610 |
| Method: | Least Squares | F-statistic: | 312.1 |
| Date: | Fri, 05 Feb 2021 | Prob (F-statistic): | 1.47e-42 |
| Time: | 22:54:00 | Log-Likelihood: | -519.05 |
| No. Observations: | 200 | AIC: | 1042. |
| Df Residuals: | 198 | BIC: | 1049. |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 7.0326 | 0.458 | 15.360 | 0.000 | 6.130 | 7.935 |
| TV | 0.0475 | 0.003 | 17.668 | 0.000 | 0.042 | 0.053 |
| Omnibus: | 0.531 | Durbin-Watson: | 1.935 |
|---|---|---|---|
| Prob(Omnibus): | 0.767 | Jarque-Bera (JB): | 0.669 |
| Skew: | -0.089 | Prob(JB): | 0.716 |
| Kurtosis: | 2.779 | Cond. No. | 338. |
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Régression linéaire multiple¶
La régression linéaire simple est une approche utile pour prédire une variable réponse sur la base d’une seule variable explicative. Cependant, dans la pratique, nous avons souvent plus d’un prédicteur. Par exemple, dans les données sur la publicité, nous avons examiné la relation entre les ventes et la publicité télévisée. Nous disposons également de données sur les sommes dépensées en publicité à la radio et dans les journaux, et nous souhaiterions peut-être savoir si l’un ou l’autre de ces deux médias est associé aux (plus ou moins) aux recettes des ventes.
Au lieu d’ajuster un modèle de régression linéaire simple distinct pour chaque prédicteur, une meilleure approche consiste à étendre le modèle de régression linéaire simple Y=β0+β1X+ϵ afin qu’il puisse directement s’adapter à de multiples prédicteurs. Nous pouvons le faire en donnant à chaque prédicteur un coefficient de pente distinct dans un modèle unique. En général, supposons que nous ayons p prédicteurs distincts. Le modèle de régression linéaire multiple prend alors la forme
où Xj représente le jème prédicteur et βj quantifie l’association entre cette variable et la réponse. Nous interprétons βj comme l’effet moyen sur Y d’une augmentation d’une unité de Xj, en maintenant fixes tous les autres prédicteurs. Dans l’exemple de la publicité, (3.5) devient
Estimation des coefficients de régression¶
Exemple 1¶
Les valeurs de ˆβ0,ˆβ0,…,ˆβp sont la solution qui minimiste l’équation \ref{argminRSS}. Tout logiciel statistique peut être utilisé pour calculer ces estimations de ces coefficients.
est = smf.ols('Sales ~ TV + Radio + Newspaper', advertising).fit()
est.summary().tables[1]
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 2.9389 | 0.312 | 9.422 | 0.000 | 2.324 | 3.554 |
| TV | 0.0458 | 0.001 | 32.809 | 0.000 | 0.043 | 0.049 |
| Radio | 0.1885 | 0.009 | 21.893 | 0.000 | 0.172 | 0.206 |
| Newspaper | -0.0010 | 0.006 | -0.177 | 0.860 | -0.013 | 0.011 |
Exemple 2¶
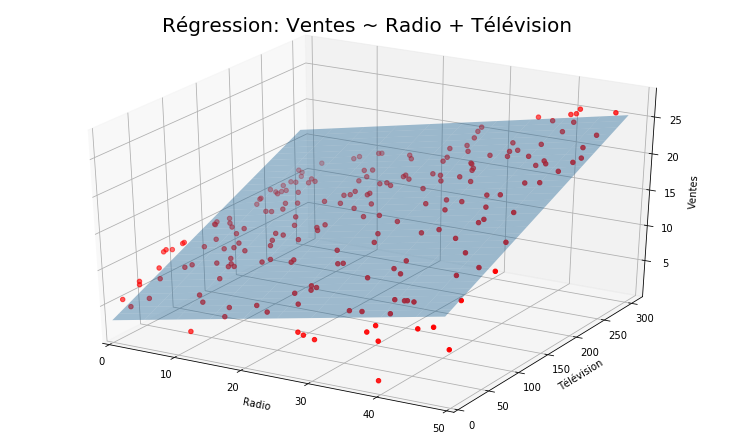
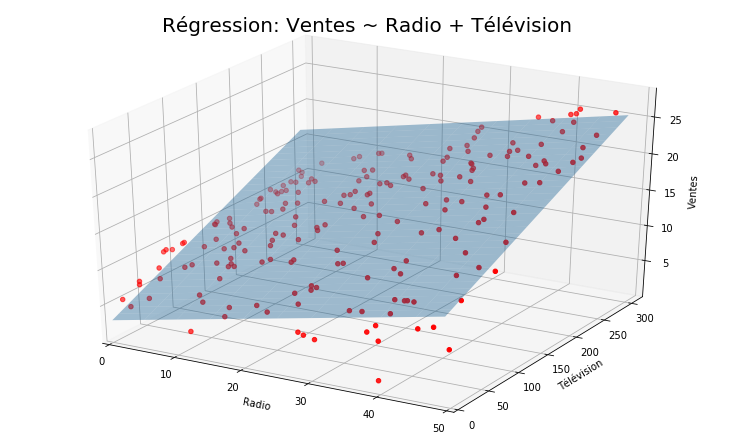
Appliquons maintenat une régression linéaire multiple sur les deux prédicteurs ‘Radio’, ‘TV’
regr = skl_lm.LinearRegression()
X = advertising[['Radio', 'TV']].values
y = advertising.Sales
regr.fit(X,y)
print(regr.coef_)
print(regr.intercept_)
[0.18799423 0.04575482]
2.9210999124051398
Traçons maintenant un graphique (3D) d’une régression linéaire effectuée sur les ventes en utilisant la télévision et la radio comme prédicteurs.
from mpl_toolkits.mplot3d import axes3d
Radio = np.arange(0,50)
TV = np.arange(0,300)
B1, B2 = np.meshgrid(Radio, TV, indexing='xy')
Z = np.zeros((TV.size, Radio.size))
for (i,j),v in np.ndenumerate(Z):
Z[i,j] =(regr.intercept_ + B1[i,j]*regr.coef_[0] + B2[i,j]*regr.coef_[1])
/Users/nourmp/anaconda3/envs/vbook4/lib/python3.7/site-packages/ipykernel_launcher.py:12: MatplotlibDeprecationWarning:
The `ymin` argument was deprecated in Matplotlib 3.0 and will be removed in 3.2. Use `bottom` instead.
