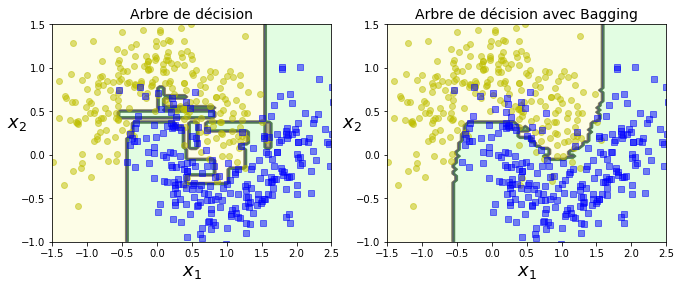
Nous avons vu que les arbres de décisions peuvent conduire à des résultats complètement différent différents suite au léger changement des données. Pour cette raison, les statisticiens ont pensé construire toute une famille d’estimateurs d’arbres qui deviendraient plus stables en moyenne (aggrégation).
Bagging¶
L’algorithme bagging pour bootstrap aggregating a été introduit par \cite{Breiman1996}. Il permet d’abord de réduire la variance, et donc réduire l’erreur de prédiction. Ces principes s’appliquent à toutes les méthodes de modélisation telles que la régression ou la classification. Toutefois, ils sont plutôt associés aux arbres de décision comme modèle de base.
Rappelons-nous que si nous avons un ensemble de \(n\) observations indépendantes, \(Z_1, Z_2, \dots , Z_n\) chacune avec une variance \(\sigma^2\), alors la variance de la moyenne \(\bar{Z}\) des observations est donné par \(\sigma^2/n\). Cette nouvelle variance est réduite de \(n\). Or, si nous appliquons ce concept aux arbres de décision, nous créons plusieurs arbres de décision appliqués sur plusieurs données d’entraînement. Ainsi le résultat de prédiction devient beaucoup moins variable. Toutefois, ce n’est pas très pratique, car nous ne pouvons pas disposer de \(n\) parties de données d’entraînement.
Nous pouvons toutefois appliquer la méthode bootsrap que nous avons vue dans les sections précédentes, nous faisons un échantillonnage avec remise sur la partie des données d’entraînement afin de créer \(B\) pseudo-parties de données d’entraînement, nous appliquons un arbre de régression sur chaque échantillon afin d’avoir \(\hat{f}^{*b} (x)\) qui est la prédiction au point \(x\).
Soit \(Y\) une variable réponse qui peut prendre des valeurs numérique ou qualitative, \(X_1, X_2, \dots , X_p\) des variables explicatives et \(f(x)\) un modèle de fonction \(x=\left\{ x_1, x_2, \dots , x_p \right\} \in \mathbb{R}_p\), on note \(n\) le nombre d’observations et
un échantillon de loi \(F\). Si nous tirons \(B\) échantillons indépendants notés \(\left\{z_b\right\}_{b=1,B}\), la prédiction par agrégation de modèles est alors définie comme
Dans le cas où la variable réponse \(Y\) est quantitative. Cette méthode est alors appelée bagging \cite{wuthrich2017data}. Ainsi, elle réduit la variance et donc l’erreur de prédiction. Toutefois, considérer \(B\) échantillons indépendants est irréaliste, il faudrait alors un très grand nombre de données. L’algorithme bagging est présenté ci-dessous;
Exemple;¶
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=500, noise=0.30, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
bag_clf = BaggingClassifier(
DecisionTreeClassifier(random_state=42), n_estimators=500,
max_samples=100, bootstrap=True, n_jobs=-1, random_state=42)
bag_clf.fit(X_train, y_train)
y_pred = bag_clf.predict(X_test)
from sklearn.metrics import accuracy_score
print(accuracy_score(y_test, y_pred))
0.904
tree_clf = DecisionTreeClassifier(random_state=42)
tree_clf.fit(X_train, y_train)
y_pred_tree = tree_clf.predict(X_test)
print(accuracy_score(y_test, y_pred_tree))
0.856
