Complexité de calcul¶
La forme fermée de régression linéaire, ˆβ=(xTx)−1xTy, ou closed form formula en anglais est très utilisé lorsque nous avons des petites matrices de données. Cependant, elle présente certains problèmes qui la rendent sous-optimale en pratique. L’inversion de la matrice est lente pour les grandes matrices et sujets à l’instabilité numérique.
Mais il existe une autre façon de formuler et de résoudre les problèmes de régression linéaire, qui s’avère meilleure dans la pratique. Cette approche permet d’obtenir des algorithmes plus rapides, des résultats numériques plus robustes et peut être facilement adaptée à d’autres algorithmes d’apprentissage. Elle modélise la régression linéaire comme un problème d’ajustement des paramètres, et déploie des algorithmes de recherche pour trouver les meilleures valeurs possibles pour les estimateurs.
On a vu dans la section précédente que dans la régression linéaire, nous recherchons la droite qui correspond le mieux aux points, sur tous les ensembles possibles de coefficients. Plus précisément, nous recherchons la droite y=f(x) qui minimise la somme des erreurs quadratiques sur toutes les observations d’entraînement, c’est-à-dire le vecteur de coefficient w qui minimise.
Plus concrètement, commençons par le cas où nous essayons de modéliser y comme une fonction linéaire d’une seule variable ou x, donc y=f(x) signifie y=w0+w1x. Pour définir la droite de régression, il faut choisir la paire de paramètres (w0,w1) qui minimise l’erreur, le coût ou la perte, c’est-à-dire la somme des carrés d’écart entre les vraies valeurs et la droite (les valeurs prédites).
Note
Ici on change la notation par rapport à la section précédente (w au lieu de β) afin d’introduire la notion des poids que nous verrons plus souvent dans les sections à venir.
Chaque paire de valeurs possibles pour (w0,w1) définira une droite, mais nous voulons vraiment les valeurs qui minimisent la fonction d’erreur ou de perte J(w0,w1 où
La somme des erreurs quadratiques devrait être claire, mais d’où vient le 1/(2n) ? Le 1/n transforme cela en une erreur moyenne, et le 1/2 est une convention courante pour des raisons techniques. En vérité, c’est que lorsque nous ferons la dérivée (nous verrons pourquoi un peu plus tard) les 2 s’annulent. Mais il faut bien comprendre que le 1/(2n) n’affecte en rien les résultats de l’optimisation. Ce multiplicateur sera le même pour chaque paire (w0,w1), et n’a donc aucune influence sur le choix des paramètres.
Alors comment trouver les bonnes valeurs pour w0 et w1 ? Nous pourrions essayer des paires de valeurs aléatoires, et garder celle qui obtient le meilleur score, c’est-à-dire avec une perte minimale J(w0,w1). Mais il semble très peu probable de tomber sur la meilleure ou même sur une solution parfaite. Pour effectuer une recherche plus systématique, nous devrons tirer parti d’une propriété spéciale qui se cache dans la fonction de perte.
Convex Parameter Spaces¶
La figure ci-dessous montre comment l’erreur d’ajustement (perte) varie avec w. Ce qui est intéressant, c’est que la fonction d’erreur a la forme d’une sorte de parabole. Elle atteint une seule valeur minimale au bas de la courbe. La coordonnée x de ce point minimum définit la meilleure pente w pour la droite de régression.
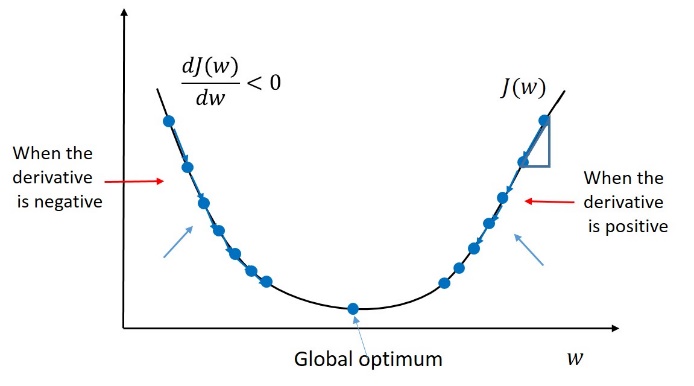
Toute surface convexe a exactement un minimum local. De plus, pour tout espace de recherche convexe, il est assez facile de trouver ce minimum : il suffit de marcher vers le bas jusqu’à ce que vous le touchiez. De chaque point de la surface, on peut faire un petit pas jusqu’à un point proche de la surface. Certaines directions nous mèneront vers une valeur plus élevée, mais d’autres nous feront descendre. Si nous pouvons identifier quel pas nous mènera plus bas, nous nous rapprocherons des minima. Et cette direction existe toujours, sauf lorsque nous nous trouvons sur le point minimal lui-même !
Comment savoir si une fonction donnée est convexe ? Souvenons-nous de l’époque du CÉGEP lorsqu’on nous a appris à faire des dérivées la dérivée f′(x) d’une fonction f(x), qui correspond à la valeur de la pente de la surface de f(x) en tout point. Chaque fois que cette dérivée était nulle, cela signifiait que nous avions atteint un point d’intérêt, qu’il s’agisse d’un maximum local ou d’un minimum. Rappelez-vous la dérivée second f′′(x), qui était la fonction dérivée de la dérivée f′(x). Selon le signe de cette dérivée second f′′(x),, vous pouvez identifier si vous atteignez un maximum ou un minimum.
Conclusion : l’analyse de ces dérivées peut nous dire quelles fonctions sont et ne sont pas convexes. Nous n’approfondirons pas ici. Mais une fois qu’il a été établi que notre fonction de perte est convexe, nous savons que nous pouvons faire confiance à un procédé comme la recherche par GD, qui nous permet d’atteindre l’optima global en marchant vers le bas.
Recherche sur Gradient Descent¶
Nous pouvons trouver les minima d’une fonction convexe simplement en partant d’un point arbitraire, et en marchant de façon répétée vers le bas. Il n’y a qu’un seul point là où il n’y a pas d’issue, c’est ce point qui définit les paramètres de la droite de régression la mieux adaptée.
Mais comment trouver une direction qui nous mène en bas de la pente ? Là encore, considérons d’abord le cas d’une seule variable, de sorte que nous recherchons la pente w1 de la droite la mieux adaptée où w0=0. Supposons que notre pente candidate actuelle soit x0. Dans ce cadre unidimensionnel restrictif, nous ne pouvons nous déplacer que vers la gauche ou vers la droite. Essayez de faire un petit pas dans chaque direction, c’est-à-dire les valeurs x0−ϵ et x0+ϵ. Si la valeur de J(0,x0−ϵ)<J(0,x0), alors nous devrions nous déplacer vers la gauche pour descendre. Si J(0,x0+ϵ)<J(0,x0), alors nous devrions nous déplacer vers la droite. Si aucun des deux n’est vrai, cela signifie que nous n’avons pas d’endroit où aller pour réduire J, et que nous devons donc avoir trouvé le minima.
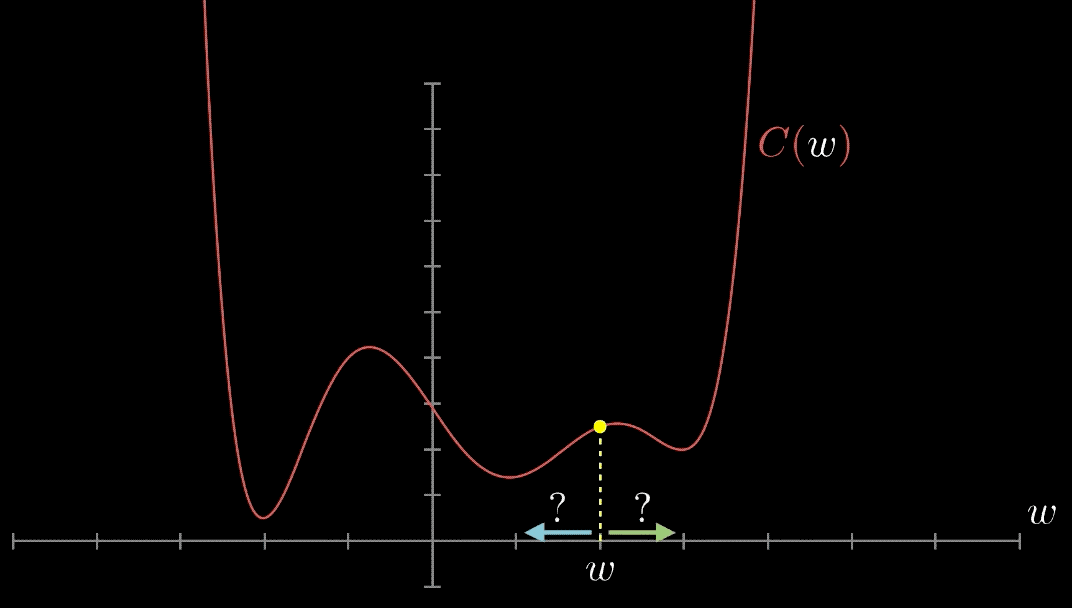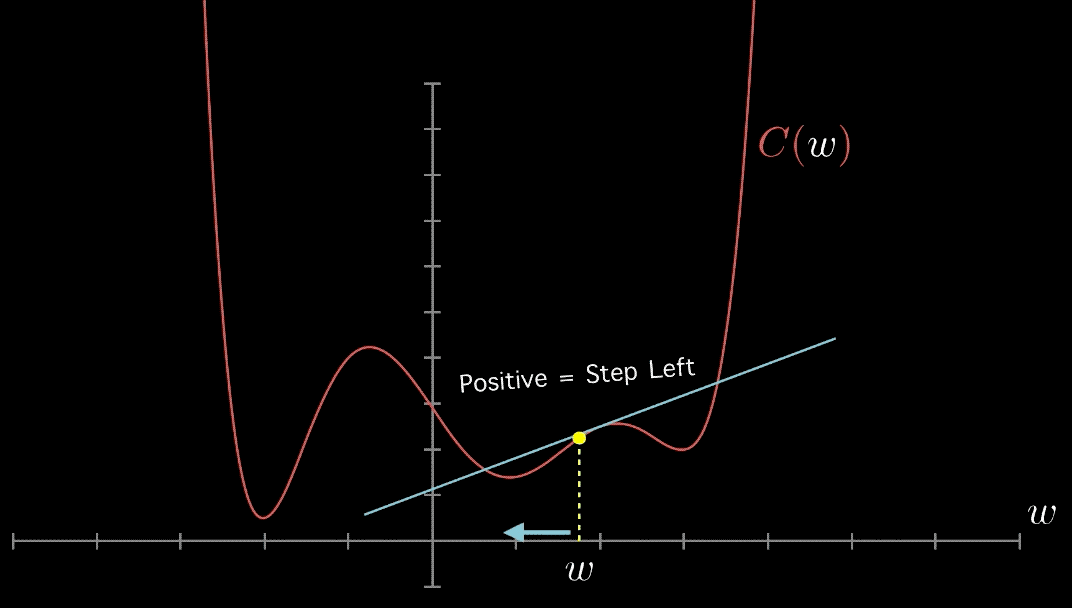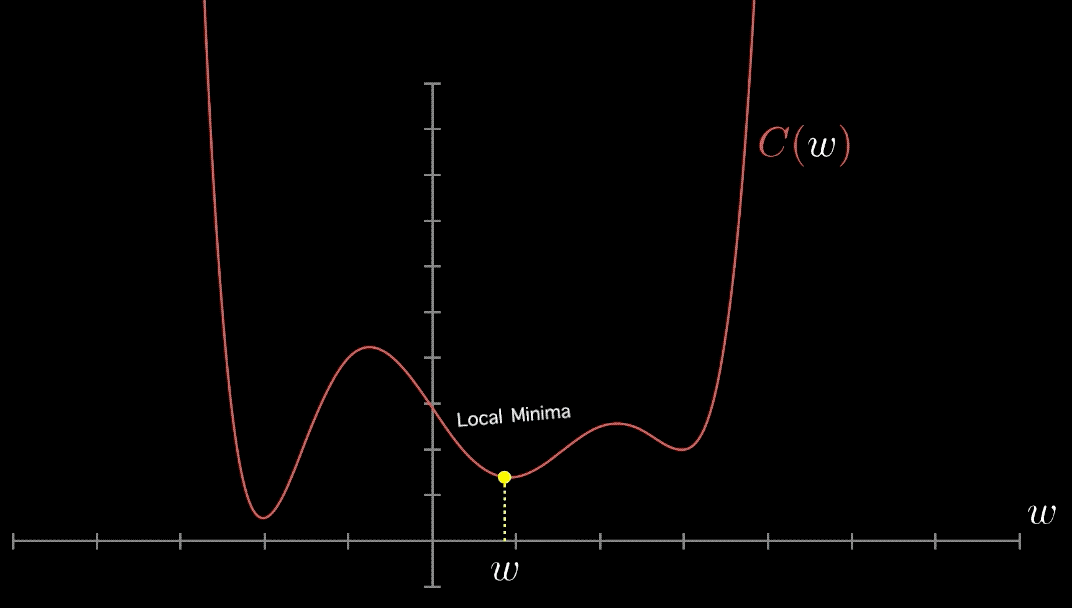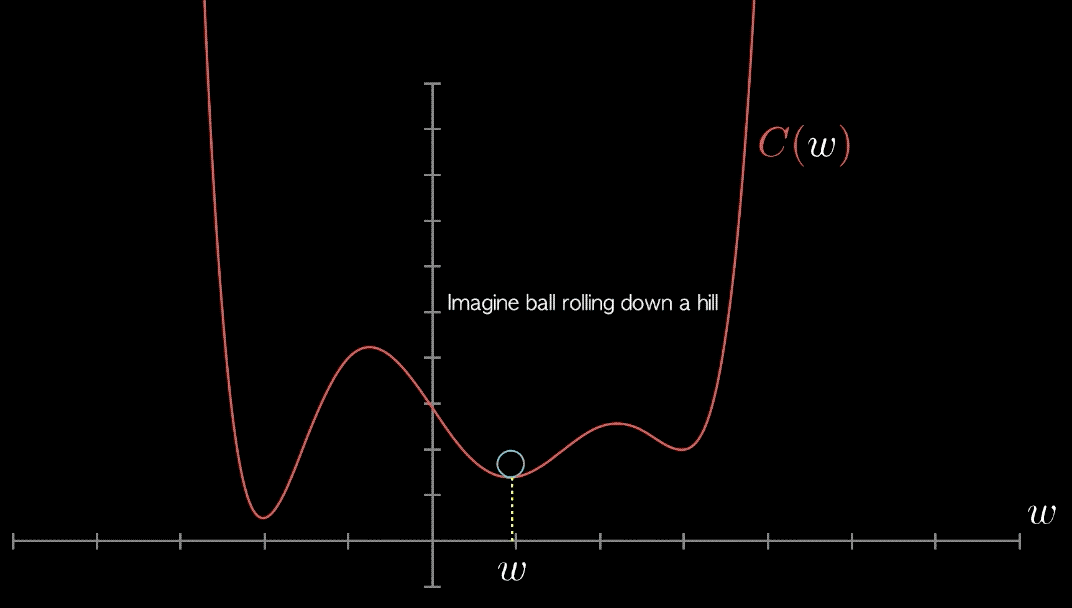
La direction vers le bas à f(x0) est définie par la pente de la droite tangente à ce point. Une pente positive signifie que les minima doivent se trouver à gauche, tandis qu’une pente négative les place à droite. L’ampleur de cette pente décrit la pente de cette chute : de combien J(0,x0−ϵ) diffère-t-il de J(0,x0)?
Cette pente peut être estimée en trouvant la droite unique qui passe par les points (x0,J(0,x0)) et (x0,J(0,x0−ϵ)), comme le montre la figure ci-dessous. C’est exactement ce qui est fait dans le calcul de la dérivée, qui à chaque point spécifie la tangente à la courbe.
Lorsque nous dépassons une dimension, nous acquérons la liberté de nous déplacer dans un plus grand nombre de directions. Les mouvements diagonaux nous permettent de traverser plusieurs dimensions à la fois. Mais en principe, nous pouvons obtenir le même effet en effectuant plusieurs pas, le long de chaque dimension distincte dans une direction orientée sur un axe. Pensez à la distance de Manhattan, où nous pouvons nous rendre où nous voulons en nous déplaçant par une combinaison de pas nord-sud et est-ouest.

Pour trouver ces directions, il faut calculer la dérivée partielle de la fonction objectif le long de chaque dimension,
Pseudocode pour la recherche de régression par Gradient Descent. La variable t indique l’itération du calcul.
Quel est le bon taux d’apprentissage ?¶
La dérivée de la fonction de perte nous indique la bonne direction pour marcher vers les minima, ce qui spécifie les paramètres pour résoudre notre problème de régression. Mais elle ne nous indique pas la distance à parcourir. La valeur de cette direction diminue avec la distance. Il est vrai que le moyen le plus rapide de se rendre à Brossard depuis Montréal est de se diriger vers le sud, mais à un moment donné, il faudra des instructions plus détaillées. La recherche en descente se fait par étapes : trouver la meilleure direction, faire un pas, puis répéter jusqu’à ce que l’on atteigne la cible. La taille de notre pas s’appelle le taux d’apprentissage, et il définit la vitesse à laquelle nous trouvons les minima. En faisant de petits pas et en consultant la carte de façon répétée (c’est-à-dire les dérivées partielles), nous y parviendrons effectivement, mais très lentement.
Cependant, de plus grands pas ce n’est pas mieux. Si le taux d’apprentissage est trop élevé, nous risquons de dépasser les minima, comme le montre la figure ci-dessous. Cela peut signifier une progression lente vers le bas à mesure que nous le dépassons à chaque étape, ou même une progression négative lorsque nous finissons par atteindre une valeur de J(w) supérieure à celle que nous avions auparavant.

En principe, nous voulons un taux d’apprentissage important au début de notre recherche, mais qui diminue à mesure que nous nous rapprochons de notre objectif. Nous devons surveiller la valeur de notre fonction de perte au cours de l’optimisation. Si les progrès deviennent trop lents, nous pouvons augmenter la taille du pas d’un facteur multiplicatif (disons 3) ou abandonner : en acceptant les valeurs actuelles des paramètres pour notre ligne d’ajustement comme étant suffisamment bonnes. Mais si la valeur de J(w) augmente, cela signifie que nous avons dépassé notre objectif. La taille de notre pas était donc trop importante, et nous devrions réduire le taux d’apprentissage par un facteur multiplicatif : disons par 1/3.
La forme de la surface fait une grande différence quant à la réussite de la recherche par GD pour trouver le minimum global. Si notre surface en forme de bol était relativement plate, comme une assiette, le point vraiment le plus bas pourrait être masqué par un nuage de bruit et d’erreur numérique. Même si nous finissons par trouver les minima, cela pourrait nous prendre très longtemps pour y arriver.
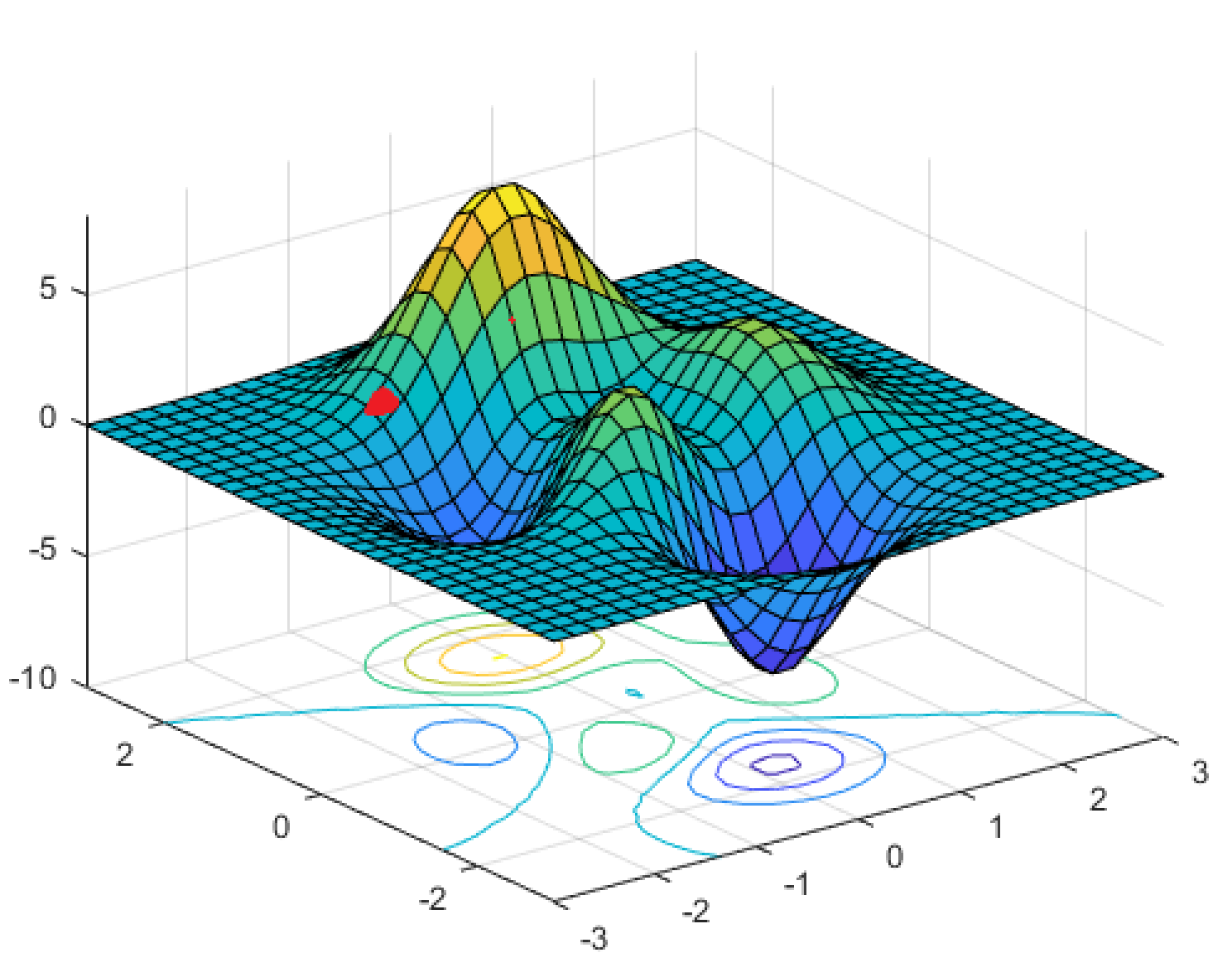
Cependant, des choses encore pires se produisent lorsque notre fonction de perte n’est pas convexe, ce qui signifie qu’il peut y avoir de nombreux minima locaux, comme dans la figure ci-dessous. Cela ne peut pas être le cas pour la régression linéaire, mais cela se produit pour de nombreux autres problèmes intéressants d’apprentissage machine.
La régression SGD en Python¶
Maintenant que vous avez une compréhension approfondie de la régression linéaire basée sur les gradients, regardons comment on peut coder tout cela en Python;
Ensuite, nous continuons avec la fonction de réévaluation du w, avec un pas de descente en pente, comme suit :
def update_weights_gd(X_train, y_train, weights, learning_rate):
""" Update weights by one step
Args:
X_train, y_train (numpy.ndarray, training data set)
weights (numpy.ndarray)
learning_rate (float)
Returns:
numpy.ndarray, updated weights
"""
predictions = compute_prediction(X_train, weights)
weights_delta = np.dot(X_train.T, y_train - predictions)
m = y_train.shape[0]
weights += learning_rate / float(m) * weights_delta
return weights
Ensuite, nous ajoutons la fonction qui calcule le coût J(w) :
Maintenant, mettez toutes les fonctions ensemble avec une fonction de _training_comme suit:
Mettre à jour le vecteur de poids à chaque itération
Imprimer le coût actuel pour chaque 100 itérations (ou n’importe quel nombre) pour vous assurer que le coût diminue et que les choses sont sur la bonne direction
Voyons comment cela se fait en exécutant les commandes suivantes :
def train_linear_regression(X_train, y_train, max_iter, learning_rate, fit_intercept=False):
""" Train a linear regression model with gradient descent
Args:
X_train, y_train (numpy.ndarray, training data set)
max_iter (int, number of iterations)
learning_rate (float)
fit_intercept (bool, with an intercept w0 or not)
Returns:
numpy.ndarray, learned weights
"""
if fit_intercept:
intercept = np.ones((X_train.shape[0], 1))
X_train = np.hstack((intercept, X_train))
weights = np.zeros(X_train.shape[1])
for iteration in range(max_iter):
weights = update_weights_gd(X_train, y_train, weights, learning_rate)
return weights
Enfin, on prédit les résultats des nouvelles valeurs d’entrée en utilisant le modèle entrainé comme suit :
Essayons le tout avec l’exemple de la section précédente.
[232.22305668 123.87481969 166.12805033 170.23901231 228.12868839
154.95746522 101.09058779 87.33631249 143.68332296 190.29353122
198.00676871 149.63039042 169.56066651 109.01983998 161.98477191
133.00870377 260.1831988 101.52551082 115.76677836 120.7338523
219.62602446 62.21227353 136.29989073 122.27908721 55.14492975
191.50339388 105.685612 126.25915035 208.99755875 47.66517424]
import numpy as np
import plotly.offline as plyo
import cufflinks as cf
import pandas as pd
cf.go_offline()
cf.set_config_file(offline=False, world_readable=True)
plyo.init_notebook_mode(connected=True)
import plotly.graph_objs as go
from IPython.core.display import display, HTML
from plotly.offline import download_plotlyjs, init_notebook_mode, plot, iplot
Batch Gradient Descent¶
Pour mettre en oeuvre la méthode Gradinet Descent, il faut calculer le gradient de la fonction de coût pour chaque paramètre du modèle θj. En d’autres termes, vous devez calculer de combien la fonction de coût changera si vous modifiez un tout petit peu θj. C’est ce qu’on appelle une dérivée partielle. C’est comme si l’on demandait “quelle est la pente de la montagne sous mes pieds si je suis tourné vers l’est”, puis que l’on posait la même question en regardant vers le nord (et ainsi de suite pour toutes les autres dimensions, si l’on peut imaginer un univers à plus de trois dimensions).
l’équation ci-dessous calcule la dérivée partielle de la fonction de coût par rapport au paramètre θj, noté ∂∂θjMSE(θ)
Au lieu de calculer ces gradients individuellement, vous pouvez utiliser les équations ci-dessous pour les calculer en une seule fois. Le vecteur de gradient, noté ∇θMSE(θ), contient toutes les dérivées partielles de la fonction de coût (une pour chaque paramètre du modèle).
Note
Notez que cette formule implique des calculs sur l’ensemble de l’entraînement X, à chaque étape de GD ! C’est pourquoi l’algorithme est appelé Batch Gradient Descent : il utilise le lot complet de données d’entraînement à chaque étape. Il est donc terriblement lent pour les très grands ensembles d’entraînement (mais nous verrons bientôt des algorithmes de GD beaucoup plus rapides). Cependant, le GD s’adapte bien au nombre de caractéristiques ; l’entraînement d’un modèle de régression linéaire lorsqu’il y a des centaines de milliers de caractéristiques est beaucoup plus rapide.
Une fois que vous avez le vecteur de gradient, qui indique la montée, il suffit d’aller dans la direction opposée pour descendre. Cela signifie qu’il faut soustraire ∇θMSE(θ) de θ. C’est là que le taux d’apprentissage entre en jeu: multiplier le vecteur de gradient par η pour déterminer la taille du pas de “descente” (voir l’équation ci-dessous)
Pour trouver un bon taux d’apprentissage, vous pouvez utiliser la recherche par grille. Cependant, vous pouvez limiter le nombre d’itérations afin que la recherche par grille puisse éliminer les modèles qui prennent trop de temps à converger.
Vous vous demandez peut-être comment fixer le nombre d’itérations. S’il est trop faible, vous serez encore loin de la solution optimale lorsque l’algorithme s’arrêtera, mais s’il est trop élevé, vous perdrez du temps pendant que les paramètres du modèle ne changent plus. Une solution simple consiste à fixer un très grand nombre d’itérations, mais à interrompre l’algorithme lorsque le vecteur de gradient devient petit, c’est-à-dire lorsque sa norme devient plus petite qu’un nombre minuscule ϵ (appelé tolérance), car cela se produit lorsque le GD a (presque) atteint le minimum.
Stochastic Gradient Descent¶
Le principal problème avec le Batch Gradient Descent est qu’il utilise l’ensemble de l’entraînement pour calculer les gradients à chaque étape, ce qui la rend très lente lorsque l’ensemble d’entraînement est grand. À l’extrême opposé, la méthode Stochastic Gradient Descent choisit une instance aléatoire de l’ensemble d’entraînement à chaque étape et calcule les gradients en se basant uniquement sur cette seule instance. De toute évidence, cela rend l’algorithme beaucoup plus rapide puisqu’il ne dispose que de très peu de données à manipuler à chaque itération. Il permet également de s’entraîner sur d’énormes ensembles d’entraînement, puisqu’une seule instance doit être en mémoire à chaque itération.
D’autre part, en raison de sa nature stochastique (c’est-à-dire aléatoire), cet algorithme est beaucoup moins régulier que Batch Gradient Descent : au lieu de descendre doucement jusqu’à atteindre le minimum, la fonction de coût rebondit de haut en bas, ne diminuant qu’en moyenne. Au fil du temps, elle finira par se rapprocher du minimum, mais une fois qu’elle y sera, elle continuera à rebondir, sans jamais se stabiliser. Ainsi, une fois que l’algorithme s’arrête, les valeurs finales des paramètres sont bonnes, mais pas optimales.
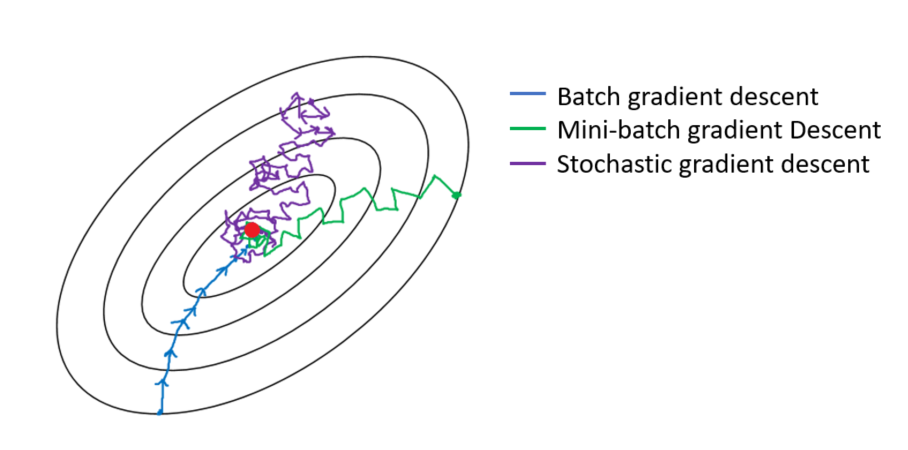
Lorsque la fonction de coût est très irrégulière (comme dans la figure 4-6), cela peut en fait aider l’algorithme à sortir des minima locaux, de sorte que le GD stochastique a plus de chances de trouver le minimum global que le Batch GD.
Le hasard est donc bon pour échapper aux optima locaux, mais mauvais car il signifie que l’algorithme ne peut jamais s’établir au minimum. Une solution à ce dilemme est de réduire progressivement le taux d’apprentissage. Les étapes commencent en grand (ce qui permet de progresser rapidement et d’échapper aux minima locaux), puis deviennent de plus en plus petites, ce qui permet à l’algorithme de s’installer au minimum global. Ce processus est appelé simulated annealing, car il ressemble au processus de recuit en métallurgie où le métal fondu est lentement refroidi. La fonction qui détermine le taux d’apprentissage à chaque itération est appelée learning schedule. Si le rythme d’apprentissage est réduit trop rapidement, vous pouvez vous retrouver bloqué dans un minimum local. Si le rythme d’apprentissage est réduit trop lentement, vous risquez de contourner le minimum pendant une longue période et de vous retrouver avec une solution sous-optimale si vous arrêtez la formation trop tôt.
n_epochs = 50
t0, t1 = 5, 50 # learning schedule hyperparameters
def learning_schedule(t):
return t0/(t+t1)
theta = np.random.randn(2,1) # random initialization
for epoch in range(n_epochs):
for i in range(m):
random_index = np.random.randint(m)
xi = X_b[random_index:random_index+1]
yi = y[random_index:random_index+1]
gradients = 2 * xi.T.dot(xi.dot(theta) - yi)
eta = learning_schedule(epoch * m + i)
theta = theta - eta * gradients
Notez que comme les instances sont choisies au hasard, certaines instances peuvent être choisies plusieurs fois par epoch, tandis que d’autres peuvent ne pas être choisies du tout. Si vous voulez être sûr que l’algorithme passe par toutes les instances à chaque epoch, une autre approche consiste à mélanger l’ensemble d’apprentissages, puis à le parcourir instance par instance, puis à le mélanger à nouveau, et ainsi de suite. Cependant, la convergence est généralement plus lente.
SGDRegressor(alpha=0.0001, average=False, early_stopping=False, epsilon=0.1,
eta0=0.1, fit_intercept=True, l1_ratio=0.15,
learning_rate='invscaling', loss='squared_loss', max_iter=50,
n_iter_no_change=5, penalty=None, power_t=0.25, random_state=None,
shuffle=True, tol=0.001, validation_fraction=0.1, verbose=0,
warm_start=False)
Mini-batch Gradient Descent¶
Mini-batch Gradient Descent est assez simple à comprendre une fois que l’on connaît Batch GD et SGD : à chaque étape, au lieu de calculer les gradients sur la base de l’ensemble des entraînements (comme dans Batch GD) ou sur la base d’une seule instance (comme dans Stochastic GD), Mini-batch GD calcule les gradients sur de petits ensembles aléatoires d’instances appelés mini-lots. Le principal avantage de Mini-batch GD par rapport à Stochastic GD est que vous pouvez obtenir une augmentation des performances grâce à l’optimisation matérielle des opérations de la matrice, en particulier lorsque vous utilisez des GPU.
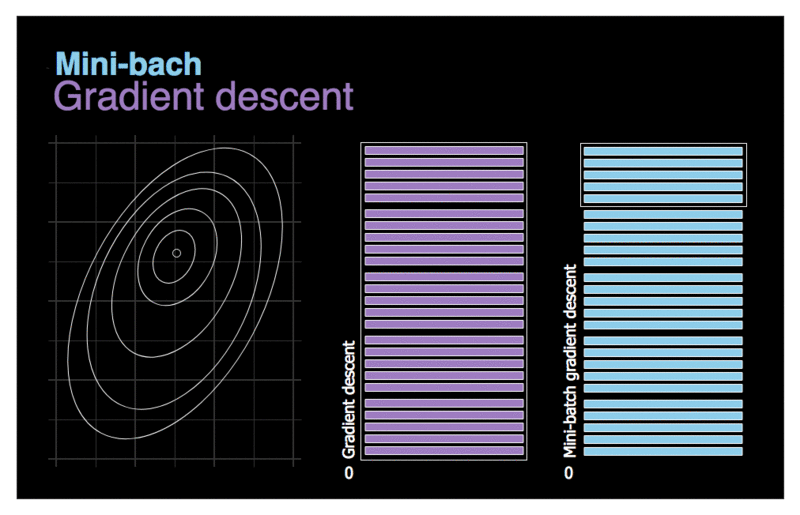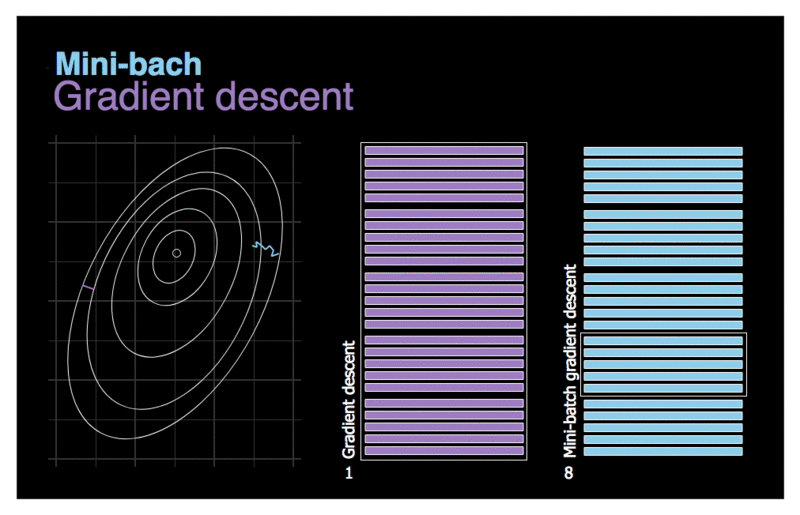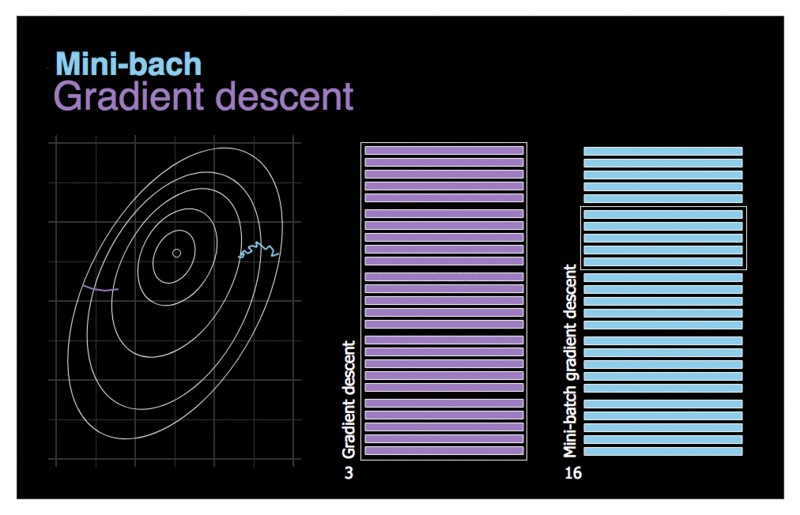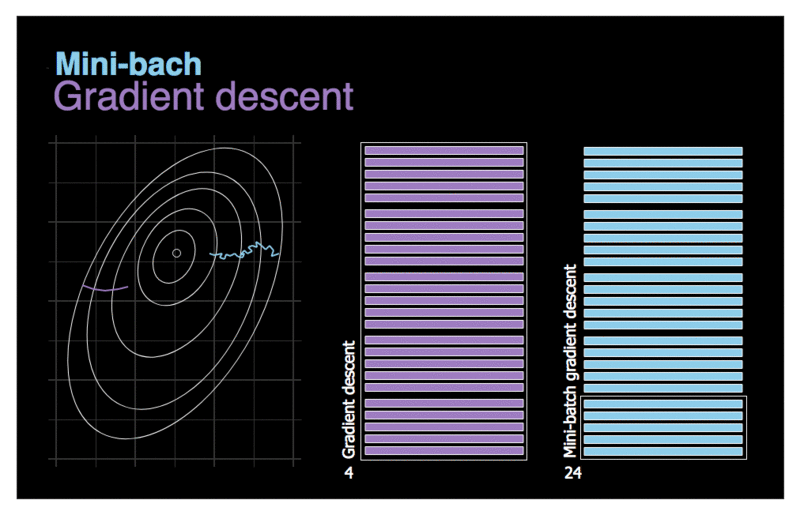
La progression de l’algorithme dans l’espace des paramètres est moins erratique qu’avec SGD, surtout avec des mini lots assez importants. Par conséquent, les mini-batchs GD finiront par se rapprocher un peu plus du minimum que SGD. Mais, d’un autre côté, il peut être plus difficile pour lui d’échapper aux minima locaux. La figure ci-dessus montre les trajectoires suivies par les trois algorithmes de GD dans l’espace des paramètres durant l’entraînement du modèle. Ils finissent tous par se rapprocher du minimum, mais le chemin de Batch GD s’arrête en fait au minimum, tandis que Stochastic GD et Mini-batch GD continuent à se déplacer. Cependant, n’oubliez pas que Batch GD prend beaucoup de temps pour faire chaque pas, et SGD et Mini-batch GD atteindraient également le minimum si vous utilisiez un bon programme d’apprentissage.
