Régularisation¶
Dans le cours STT5100, on voit des techniques de sélection de variables comme la technique de Subset Selection qui permet sélectionner un certain nombre de variables parmi \(p-1\) variables et permutant toutes les possibilités des variables dans notre modèle. Toutefois, cette tecgnique devient vite infaisable lorsque \(p\) est grand. On a aussi vu la technique Stepwise Selection, où à chaque step, une variable est considérée pour être ajoutée ou soustraite à l’ensemble des variables explicatives \(p-1\) en fonction d’un critère prédéfini (AIC), BIC, ou \(R^2\) ajusté…etc.
Avoir un riche ensemble de prédicteurs à la régression est une bonne chose, mais n’oublions pas le principe de simplicité; L’explication la plus simple repose sur le plus petit nombre de variables qui modélisent bien les données.
Idéalement, nos régressions devraient sélectionner les variables les plus importantes et les ajuster, mais la fonction objective dont nous avons parlé tente seulement de minimiser l’erreur de somme des carrés.
Nous devons donc modifier notre fonction objective. Comme alternative, nous pouvons ajuster un modèle contenant tous les \(p-1\) prédicteurs en utilisant une technique qui contraint ou “régularise” les estimations de coefficient \(\hat{\beta}\), ou de manière équivalente, qui réduit les estimations de coefficient autour zéro.
Les deux techniques les plus connues pour réduire les coefficients de régression vers zéro sont la régression de Ridge et le Lasso.
Ridge¶
La régularisation est l’astuce qui consiste à ajouter des termes secondaires à la fonction objectif pour favoriser les modèles qui gardent des coefficients faibles (ou tout près de 0).
Nous avons vu au chapitre précédent que la procédure d’ajustement des moindres carrés estime \(\beta_{0}, \beta_{1}, \ldots, \beta_{p}\) en utilisant les valeurs qui minimisent $\( \mathrm{RSS}=\sum_{i=1}^{n}\left(y_{i}-\beta_{0}-\sum_{j=1}^{p} \beta_{j} x_{i j}\right)^{2} \)$
La régularisation est l’astuce qui consiste à ajouter des termes secondaires à la fonction objectif pour favoriser les modèles qui gardent des coefficients faibles. Supposons que nous généralisons notre fonction de perte avec un deuxième ensemble de termes qui sont fonction des coefficients, et non les données d’entrainement.
Dans cette équation, nous payons une pénalité proportionnelle à la somme des carrés des coefficients utilisés dans le modèle. En élevant les coefficients au carré, nous ignorons le signe et nous nous concentrons sur la magnitude.
Le paramètre \(\lambda >0\) est le paramètre de réglage (ou le tuning parameter), il module la force relative des contraintes de régularisation. Plus \(\lambda\) est élevée, plus l’optimisation s’efforcera de réduire la taille des coefficients, au détriment de l’augmentation des résidus. Il devient finalement plus intéressant de fixer le coefficient d’une variable non corrélée à zéro, plutôt que de l’utiliser pour surajuster l’ensemble d’entrainement.
Lorsque \(\lambda=0\), le terme de pénalité n’a aucun effet, et la régression de Ridge produira les estimations des moindres carrés. Cependant, quand \(\lambda \rightarrow \infty\), l’impact de la pénalité de rétrécissement augmente, et les estimations du coefficient de régression Ridge s’approcheront de zéro. Contrairement aux moindres carrés, qui ne génèrent qu’un seul ensemble d’estimations de coefficients, la régression Ridge produira un ensemble différent de coefficients estimations,\(\hat{\beta}_{\lambda}^{R}\) , pour chaque valeur de \(\lambda\). Le choix de valeur pour \(\lambda\) est essentiel, et cela se fait avec la validation croisée.
La pénalisation de la somme des coefficients carrés, comme dans la fonction de perte ci-dessus, est appelée régression de Ridge ou régularisation de Tikhonov. En supposant que les variables dépendantes ont toutes été correctement normalisées à zéro. L’équation ci-dessous montre la solution de forme fermée (où \(\mathbf{A}\) est la matrice d’identité \((n × n)\) sauf avec un \(0\) dans la cellule supérieure gauche, correspondant au terme de biais).
Exemple Credit Data¶
Regardons l’exemple à la section 6.2.1 du livre [JWHT13]:
df_credit=pd.read_csv("https://raw.githubusercontent.com/nmeraihi/data/master/islr/Credit.csv")
df_credit.head()
| Unnamed: 0 | Income | Limit | Rating | Cards | Age | Education | Gender | Student | Married | Ethnicity | Balance | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 14.891 | 3606 | 283 | 2 | 34 | 11 | Male | No | Yes | Caucasian | 333 |
| 1 | 2 | 106.025 | 6645 | 483 | 3 | 82 | 15 | Female | Yes | Yes | Asian | 903 |
| 2 | 3 | 104.593 | 7075 | 514 | 4 | 71 | 11 | Male | No | No | Asian | 580 |
| 3 | 4 | 148.924 | 9504 | 681 | 3 | 36 | 11 | Female | No | No | Asian | 964 |
| 4 | 5 | 55.882 | 4897 | 357 | 2 | 68 | 16 | Male | No | Yes | Caucasian | 331 |
On doit ignorer la première colonne Unnamed: 0;
df_credit=df_credit.iloc[:,1:]
df_credit.head()
| Income | Limit | Rating | Cards | Age | Education | Gender | Student | Married | Ethnicity | Balance | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 14.891 | 3606 | 283 | 2 | 34 | 11 | Male | No | Yes | Caucasian | 333 |
| 1 | 106.025 | 6645 | 483 | 3 | 82 | 15 | Female | Yes | Yes | Asian | 903 |
| 2 | 104.593 | 7075 | 514 | 4 | 71 | 11 | Male | No | No | Asian | 580 |
| 3 | 148.924 | 9504 | 681 | 3 | 36 | 11 | Female | No | No | Asian | 964 |
| 4 | 55.882 | 4897 | 357 | 2 | 68 | 16 | Male | No | Yes | Caucasian | 331 |
Transformons les variables catégorielles en category;
df_credit["Gender"] = df_credit["Gender"].astype('category')
df_credit["Student"] = df_credit["Student"].astype('category')
df_credit["Married"] = df_credit["Married"].astype('category')
df_credit["Ethnicity"] = df_credit["Ethnicity"].astype('category')
from sklearn.preprocessing import scale
y = df_credit.Balance
X = df_credit[df_credit.columns.difference(['Balance'])]
X = pd.get_dummies(X, drop_first=True)
X_scaled = scale(X)
X.head(3)
| Age | Cards | Education | Income | Limit | Rating | Ethnicity_Asian | Ethnicity_Caucasian | Gender_Female | Married_Yes | Student_Yes | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 34 | 2 | 11 | 14.891 | 3606 | 283 | 0 | 1 | 0 | 1 | 0 |
| 1 | 82 | 3 | 15 | 106.025 | 6645 | 483 | 1 | 0 | 1 | 1 | 1 |
| 2 | 71 | 4 | 11 | 104.593 | 7075 | 514 | 1 | 0 | 0 | 0 | 0 |
from sklearn.linear_model import Ridge
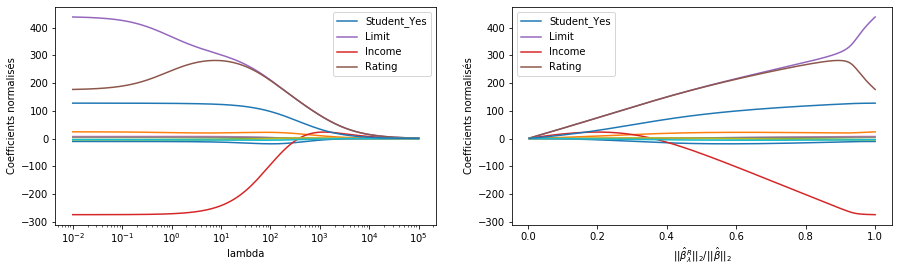
La figure de droite affiche les mêmes estimations du coefficient Ridge que celle de gauche, mais au lieu d’afficher \(\lambda\) sur l’axe \(x\), nous affichons maintenant \(||\hat{\beta}_{\lambda}^{R}||_{2} / ||\hat{\beta}||_{2},\) où \(\hat{\beta}\) désigne le vecteur des estimations du coefficient des moindres carrés. La notation \(\|\beta\|_{2}\) désigne la norme \(\ell_{2}\) (prononcée “ell 2”) d’un vecteur, et est définie comme \(\|\beta\|_{2}=\sqrt{\sum_{j=1}^{p} \beta_{j}^{2}}\). Il mesure la distance de \(\beta\) par rapport à zéro. Plus \(\lambda\) augmente, plus la norme de \(\ell_{2}\) de \(\hat{\beta}_{\lambda}^{R}\) diminuera toujours, tout comme \(||\hat{\beta}_{\lambda}^{R}||_{2} / ||\hat{\beta}||_{2},\).
Cette dernière quantité va de 1 (lorsque \(\lambda=0,\), auquel cas l’estimation du coefficient de régression Ridge est la même que celle des moindres carrés, et donc leurs normes \(\ell_{2}\) sont les mêmes) à \(0\) (lorsque \(\lambda=\infty\), auquel cas l’estimation du coefficient de régression de Ridge est un vecteur de zéros, avec la norme \(\ell_{2}\) égale à zéro). Par conséquent, nous pouvons considérer l’axe \(x\) dans la figure de sroite comme le
LASSO¶
La régression Ridge est optimisée pour sélectionner de petits coefficients. En raison de la fonction de coût de la somme des carrés, elle “punit” particulièrement les plus grands coefficients.
Bien que la régression Ridge soit efficace pour réduire l’ampleur des coefficients, ce critère ne les pousse pas vraiment à zéro et élimine totalement la variable du modèle.
Une autre solution consiste à essayer de minimiser la somme des valeurs absolues des coefficients, ce qui permet de faire baisser les plus petits coefficients comme les plus grands.
La régression LASSO (pour “Least Absolute Shrinkage and Selection Operator”) est une alternative relativement récente à la régression de Ridge qui surpasse cet inconvénient. Les coefficients du lasso, \(\hat{\beta}_{\lambda}^{L}\), minimisent la quantité
On peut remarquer une grande similitude entre l’équation Lasso et Ridge. La seule différence est que le terme \(\beta_{j}^{2}\) dans la pénalité de régression Ridge a été remplacé par \(\left|\beta_{j}\right|\) dans la pénalité du Lasso.
En effet, la régression Lasso répond à ce critère : minimiser la métrique \(\ell_{1}\) sur les coefficients au lieu de la métrique \(\ell_{2}\).
Avec LASSO, nous spécifions une contrainte explicite \(s\) quant à ce que peut être la somme des coefficients, et l’optimisation minimise la somme des erreurs quadratiques sous cette contrainte.
En langage statistique, la technique Lasso utilise une pénalité \(\ell_{1}\) au lieu d’une pénalité \(\ell_{2}\). La norme \(\ell_{1}\) d’un vecteur de coefficient \(\beta\) est donnée par \(\|\beta\|_{1}=\sum\left|\beta_{j}\right|\).
Lors que la régression Ridge on tente de résoudre:
La propriété de sélection variable du lasso¶
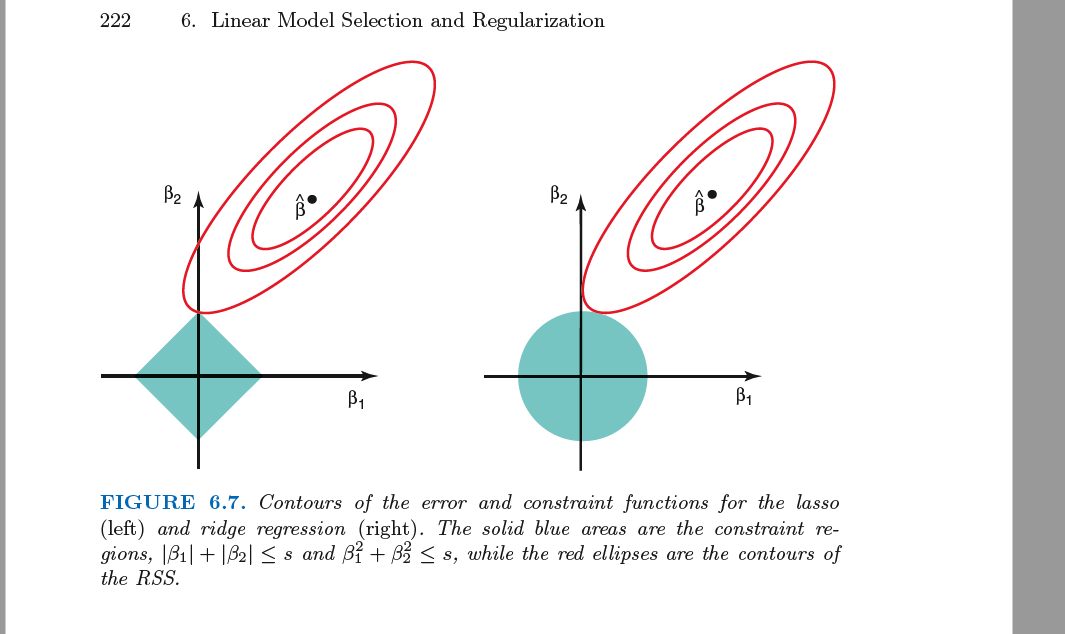
Mais pourquoi LASSO fait-elle activement passer les coefficients à zéro ? Cela a à voir avec la forme du cercle de la métrique \(\ell_{1}\).
Comme illustré dans la figure ci-dessous, la forme du cercle \(\ell_{1}\) (l’ensemble des points équidistants de l’origine) n’est pas ronde, mais possède des sommets et des caractéristiques de dimension inférieure comme des arêtes et des faces.
Si nos coefficients \(\beta\) sont contraints de se trouver à la surface d’un cercle de rayon-\(s\) \(\ell_{1}\), cela signifie qu’il est probable qu’il touche l’une de ces caractéristiques à plus faible dimension, ce qui signifie que les dimensions non utilisées obtiennent des coefficients nuls.
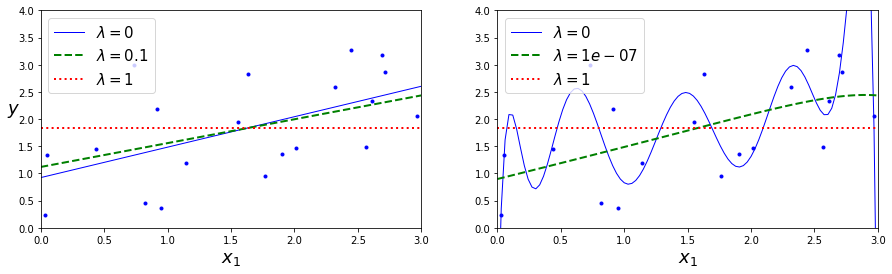
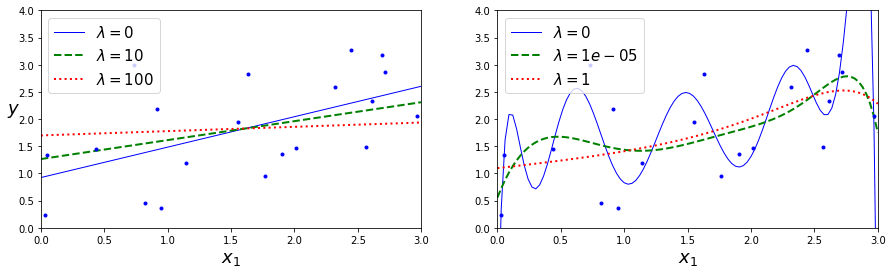
Une caractéristique importante de la régression lasso est qu’elle tend à éliminer complètement les poids des caractéristiques les moins importantes (c’est-à-dire à les mettre à zéro). Par exemple, la ligne pointillée dans le graphique ci-dessus de la figure (avec \(\lambda=10e-07\)) semble quadratique, presque linéaire : tous les poids des caractéristiques polynomiales de haut degré sont égaux à zéro. En d’autres termes, la régression lasso effectue automatiquement la sélection des variables.
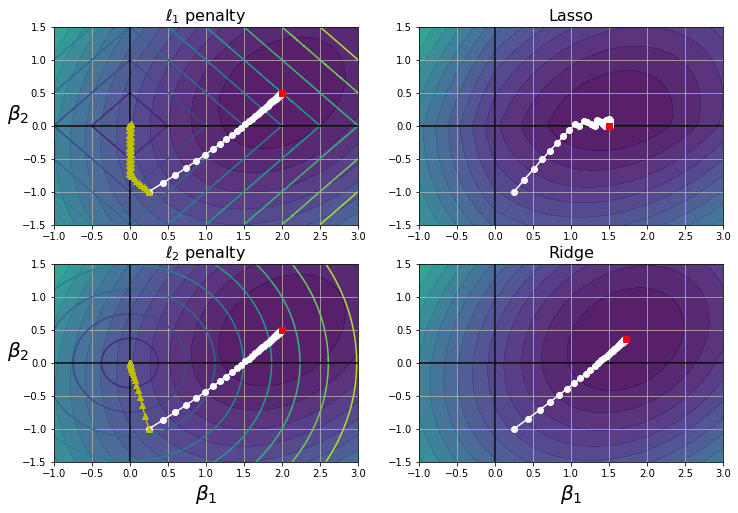
Sur le graphique de gauche, les contours de fond (ellipses) représentent une fonction de coût non régularisée du MSE \(\lambda=0\), et les cercles blancs montrent la trajectoire BGD sur cette fonction de coût. Les contours d’avant-plan (losanges) représentent la pénalité \(\ell_{1}\), et les triangles (jaunes) montrent la trajectoire BGD pour cette pénalité \((\lambda \rightarrow \infty)\).
Remarquez comment la trajectoire en premier plan atteint \(\beta_1=0\), puis descend doucement jusqu’à ce qu’elle atteigne \(\beta_2=0\). Sur le graphique en haut à droite, les contours représentent la même fonction de coût plus une pénalité de \(\ell_{1}\) avec \(\lambda=0.5\). Le minimum global se trouve sur l’axe \(\beta_2=0\). BGD atteint d’abord \(\beta_2=0\), puis descend doucement jusqu’à ce qu’elle atteigne le minimum global. Les deux graphiques du bas montrent la même chose, mais utilisent une pénalité de \(\ell_{2}\) à la place. Le minimum régularisé est plus proche de \(\beta_2=0\) que le minimum non régularisé, mais les poids ne sont pas totalement éliminés.
Elastic Net¶
Une généralisation du modèle du lasso est Elastic Net, introduit par [ZH05], qui combine à la fois les pénalités de \(\ell_{1}\) et \(\ell_{2}\). Le terme de régularisation est un simple mélange des termes de régularisation de Ridge et du Lasso, et vous pouvez contrôler le rapport de mélange \(r\). Lorsque \(r = 0\), le Elastic Net est équivalent à la régression de la Ridge, et lorsque \(r = 1\), il est équivalent à la régression du Lasso
\( \sum_{i=1}^{n}\left(y_{i}-\beta_{0}-\sum_{j=1}^{p} \beta_{j} x_{i j}\right)^{2}+r \lambda \sum_{j=1}^{n}\left|\beta_{j}\right|+\frac{1-r}{2} \beta \sum_{j=1}^{n} \beta_{j}^{2}= \operatorname{RSS}+r \lambda \sum_{j=1}^{n}\left|\beta_{j}\right|+\frac{1-r}{2} \beta \sum_{j=1}^{n} \beta_{j}^{2} \)
Sélection des paramètres calibrage¶
section 6.2.3 dans [JWHT13]
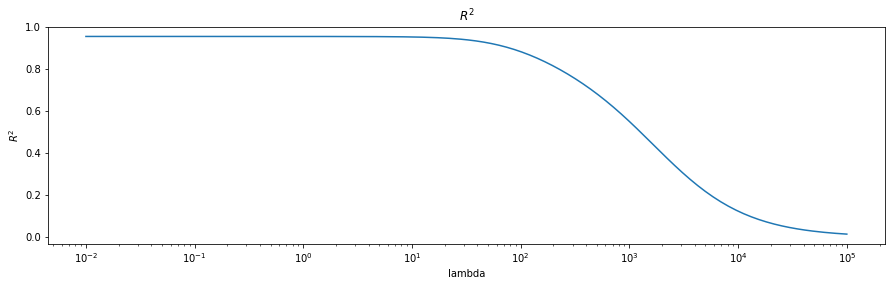
La validation croisée est un moyen simple de pour choisir le bon \(\lambda\). Nous choisissons une grille de valeurs de \(\lambda\), et nous calculons l’erreur de validation croisée pour chaque valeur de \(\lambda\).
Nous sélectionnons ensuite cette valeur pour laquelle l’erreur de validation croisée est la plus faible. Enfin, le modèle est réajusté en utilisant toutes les observations disponibles et la valeur sélectionnée du paramètre de réglage.
from sklearn.linear_model import LinearRegression, Ridge, RidgeCV, Lasso, LassoCV
from sklearn.linear_model import RidgeCV
lambdas = np.logspace(0.5, -4, 100)
ridgeCV = RidgeCV(alphas=lambdas, store_cv_values=True)
ridgeCV.fit(X_scaled, y)
MSE_alphas = np.mean(ridgeCV.cv_values_, axis=0)
fig, ax = plt.subplots(1, 1, figsize=(15,4))
ax.plot(lambdas, MSE_alphas)
ax.axvline(ridgeCV.alpha_, color='k', linestyle='--')
ax.set_xscale('log')
ax.set_xlabel(r"Lambda ($\lambda$)")
ax.set_ylabel('CV MSE');
ridgeCV.alpha_
0.3511191734215131
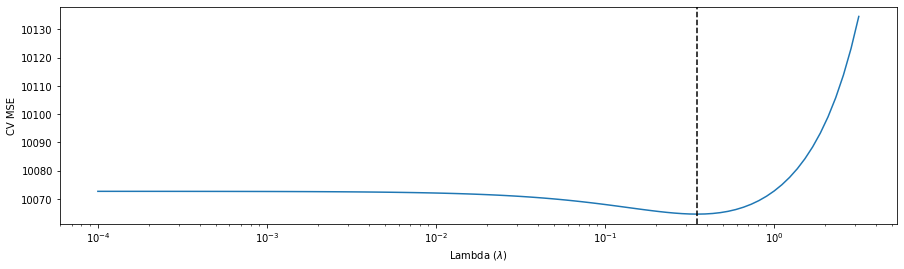
Dans la figure ci-dessus, réalise un modèle Ridge avec validation croisée sur l’ensemble des données du Crédit. La droite verticale en pointillée indique la valeur sélectionnée de \(\lambda=0.3511\).
En optimisant ces modèles sur une large gamme de valeurs pour le paramètre de régularisation approprié \(s\), nous obtenons un graphique de l’erreur d’évaluation en fonction de \(s\) comme dans l’exemple précédent.
Un bon ajustement aux données d’entrainement avec peu/petits paramètres est plus robuste qu’un ajustement légèrement meilleur avec de nombreux paramètres.
Plusieurs métriques ont été développées pour aider à la sélection des modèles. Les plus importants sont les critères d’information Akaike (AIC) et les critères d’information Baysian (BIC). ces métriques sont un moyen de comparer des modèles avec un nombre différent de paramètres.
Même si la régression LASSO/ridge punit les coefficients basés sur les poids, elle ne les met pas explicitement à zéro si vous voulez exactement \(k\) paramètres. Vous devez ensuite supprimer les variables inutiles de votre modèle.
Les variables à supprimer en premier lieu doivent être celles qui présentent:
de petits coefficients,
une faible corrélation avec la fonction objectif,
une corrélation élevée avec une autre caractéristique du modèle et
aucune relation évidente justifiable avec la variable réponse.
- JWHT13(1,2)
Gareth James, Daniela Witten, Trevor Hastie, and Robert Tibshirani. An introduction to statistical learning. Volume 112. Springer, 2013.
- ZH05
Hui Zou and Trevor Hastie. Regularization and variable selection via the elastic net. Journal of the royal statistical society: series B (statistical methodology), 67(2):301–320, 2005.