Fractionnement des données¶
On se rappelle qu’en régression, notre objectif est de trouver une fonction \(f(x)\) qui nous permet les valeurs futures de \(\mathbf{Y}\) sur la base d’un ensemble de données \(\mathbf{X}\). Afin de généraliser le plus possible notre modèle sur toute sorte de futures observations (donc nouvelles données), nous devons fractionner notre ensemble de données en deux parties. Une partie qui vous sert à entraîner votre modèle, et l’autre partie à tester la performance de votre modèle.
Un peu comme lorsque vous vous préparez pour un examen de la SOA. Si l’on vous donne les mêmes questions que ceux qu’on trouve dans les manuels de préparation (ASM, coaching actuaries … etc.). Ce serait trop facile de faire de tels examens, puisque vous aurez vu toutes les versions de questions. Or, dans la vraie vie, ça ne se passe pas vraiment comme ça. Les questions d’examen seront semblables aux situations déjà vues dans votre préparation, mais jamais (ou presque) exactement les mêmes questions.
Afin d’éviter qu’un modèle surapprenne (overfitting), on doit garder une partie des données (test data set) que le modèle n’a jamais vue pour mesurer la performance du modèle.
Training dataset :¶
Ces données sont utilisées pour travailler sur les variables explicatives, ajuster les modèles, travailler sur les hyperparamètres, comparer les modèles et en sélectionner les meilleurs candidats.
Cette partie des données représente 60-80% de nos de notre ensemble de données.
Test dataset¶
Après avoir choisi un modèle final, ces données sont utilisées pour estimer les performances du modèle, que nous appelons l’erreur de généralisation.
Cette partie des données représente 20-40% de nos de notre ensemble de données.
Échantillonnage aléatoire¶
La façon la plus simple de répartir les données entre les ensembles de formation et de test est de prendre un simple échantillon aléatoire. Cela ne permet de contrôler aucun attribut des données, comme la distribution de votre variable de réponse \(\mathbf{Y}\).
En Python, on peut utiliser le train_test_split de sklearn.
import numpy as np
from sklearn.model_selection import train_test_split
X, y = np.arange(10).reshape((5, 2)), range(5)
X
array([[0, 1],
[2, 3],
[4, 5],
[6, 7],
[8, 9]])
list(y)
[0, 1, 2, 3, 4]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=6100)
X_train
array([[8, 9],
[2, 3],
[4, 5]])
X_test
array([[0, 1],
[6, 7]])
y_train
[4, 1, 2]
y_test
[0, 3]
en R, on peut utiliser la fincton createDataPartition du package caret
Échantillonnage stratifié¶
Si nous voulons contrôler explicitement l’échantillonnage afin que nos ensembles d’entraînement et de test aient des distributions \(\mathbf{Y}\) similaires, nous pouvons utiliser un échantillonnage stratifié. Cela est plus courant pour les problèmes de classification où la variable de réponse peut être fortement déséquilibrée (par exemple, 90 % des observations avec la réponse “Oui” et 10 % avec la réponse “Non”). Cependant, nous pouvons également appliquer l’échantillonnage stratifié aux problèmes de régression.
Si vous utilisez la fonction train_test_split de sklearn, vous pouvez ajouter l’argument stratify=y.
Disparités de classe¶
Souvent, lorsqu’il s’agit de problèmes de classification, les données ne sont pas bien équilibrées. Par exemple, dans une base de données de fraude, le nombre d’observations considérées frauduleuses est en bas de 5% \(y=1\). Dans ce cas, on risque d’appliquer un modèle de classification sans considérer le fait que 95% des observations seront non-frauduleuses (\(y=0\)). En effet, supposons un modèle “assez fou” qui vous donne comme variables une prédiction \(\hat{\mathbf{y}}=0\) sur toutes les observations dans votre partie test de vos données. Lorsque vous voulez mesurer l’erreur de votre modèle, il sera 95% juste! Ce qui tout à fait absurde.
Le sous-échantillonnage permet d’équilibrer l’ensemble des données en réduisant la taille de la ou des classes dominantes pour qu’elles correspondent aux fréquences de la classe la moins répandue. Cette méthode est utilisée lorsque la quantité de données est suffisante.
L’autre technique, le suréchantillonnage, est utilisée lorsque la quantité de données est insuffisante. Il tente d’équilibrer l’ensemble des données en augmentant la taille des échantillons plus rares.
Il n’y a pas d’avantage absolu d’utiliser une méthode d’échantillonnage par rapport à une autre. L’application de ces deux méthodes dépend du cas d’utilisation auquel elle s’applique et de l’ensemble de données lui-même. Une combinaison des deux est souvent efficace et une approche commune est connue sous le nom de Synthetic Minority Over-Sampling Technique ou SMOTE [CBHK02].
Le surajustement (Overfitting)¶
Revenons à l’exemple de vous préparer à un examen de la SOA. Pour simplifier, supposons que c’est l’examen P. Supposons que vous décidez de vous pratiquer en faisant 100 questions. Avec cette pratique, vous découvrez que lorsqu’une question traite un sujet X, la réponse est toujours A dans les choix de réponse, alors que si la question concerne le sujet \(z\), la réponse est toujours C. Nous pourrions alors conclure que c’est toujours vrai et appliquer cette règle plus tard, même si le sujet ou la réponse ne concerne pas les sujets x ou z. Ou, pire encore, vous pourriez mémoriser les réponses à chaque question mot pour mot. Vous obtiendrez un score élevé aux questions du vrai examen. Cependant, en réalité, vous obtiendrez un score très faible, car il est rare que les mêmes questions soient posées lors des examens.
Le phénomène de mémorisation peut entraîner un surajustement. Cela se produit lorsque nous extrayons trop d’informations de l’ensemble des données d’entraînement et que nous faisons en sorte que notre modèle fonctionne bien, ce que l’on appelle un faible biais. On se rappelle que le biais est l’écart entre la vraie valeur d’une variable inobservable et la valeur prédite.
Où \(\hat{\mathbf{y}}\) est la valeur prédite. Le surajustement ne nous aidera pas à généraliser à de nouvelles données. Il sera peu performant sur des ensembles de données qui n’ont pas été vus auparavant.
On dit qu’il y a surajustement lorsque nous rendons le modèle excessivement complexe de sorte qu’il s’adapte à chaque échantillon d’apprentissage, par exemple la mémorisation des réponses à toutes les questions, comme mentionnée précédemment dans l’exemple de l’examen.
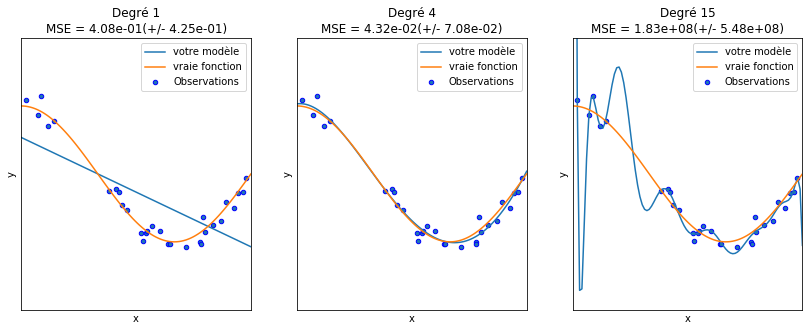
On peut bien voir cette situation dans la figure de droite de l’exemple Exemple
Sous-ajustement (Underfitting)¶
Le scénario inverse est le sous-ajustement. Lorsqu’un modèle est sous-ajusté, il n’est pas performant sur les ensembles d’entraînement et ne le sera pas sur les ensembles de tests, ce qui signifie qu’il ne parvient pas à saisir la tendance sous-jacente des données. Cela peut également se produire si nous essayons d’ajuster le mauvais modèle aux données, tout comme nous obtiendrons de mauvais résultats à des exercices ou des examens si nous adoptons la mauvaise approche d’étude. Nous appelons n’importe laquelle de ces situations un biais élevé dans l’apprentissage machine ; bien que sa variance soit faible, car les performances dans les ensembles de formation et d’examens sont assez constantes, de façon mauvaise.
On peut bien voir cette situation dans la figure de gauche de l’exemple Exemple
Exemple¶
Dans l’exemble suivant, on peut voir la différence entre un surajustement (droite) et un sous-ajustement (gauche)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
def true_fun(X):
return np.cos(1.5 * np.pi * X)
np.random.seed(0)
n_samples = 30
degrees = [1, 4, 15]
X = np.sort(np.random.rand(n_samples))
y = true_fun(X) + np.random.randn(n_samples) * 0.1
plt.figure(figsize=(14, 5))
for i in range(len(degrees)):
ax = plt.subplot(1, len(degrees), i + 1)
plt.setp(ax, xticks=(), yticks=())
polynomial_features = PolynomialFeatures(degree=degrees[i],
include_bias=False)
linear_regression = LinearRegression()
pipeline = Pipeline([("polynomial_features", polynomial_features),
("linear_regression", linear_regression)])
pipeline.fit(X[:, np.newaxis], y)
# Evaluate the models using crossvalidation
scores = cross_val_score(pipeline, X[:, np.newaxis], y,
scoring="neg_mean_squared_error", cv=10)
X_test = np.linspace(0, 1, 100)
plt.plot(X_test, pipeline.predict(X_test[:, np.newaxis]), label="votre modèle")
plt.plot(X_test, true_fun(X_test), label="vraie fonction")
plt.scatter(X, y, edgecolor='b', s=20, label="Observations")
plt.xlabel("x")
plt.ylabel("y")
plt.xlim((0, 1))
plt.ylim((-2, 2))
plt.legend(loc="best")
plt.title("Degré {}\nMSE = {:.2e}(+/- {:.2e})".format(
degrees[i], -scores.mean(), scores.std()))
plt.show()
Compromis biais-variance¶
Il est évident que nous voulons éviter à la fois le surajustement et le sous-ajustement. Rappelons que le biais est l’erreur qui découle d’hypothèses incorrectes dans l’algorithme d’apprentissage ; un biais élevé entraîne un sous-ajustement. La variance mesure la sensibilité de la prédiction du modèle aux variations des ensembles de données. Nous devons donc éviter les cas où le biais ou la variance devient élevé. Cela signifie-t-il que nous devons toujours faire en sorte que le biais et la variance soient aussi faibles que possible ? La réponse est oui, si nous le pouvons. Mais, en pratique, il existe un compromis explicite entre les deux, où le fait de diminuer l’un augmente l’autre. C’est ce que l’on appelle le compromis biais-variance.
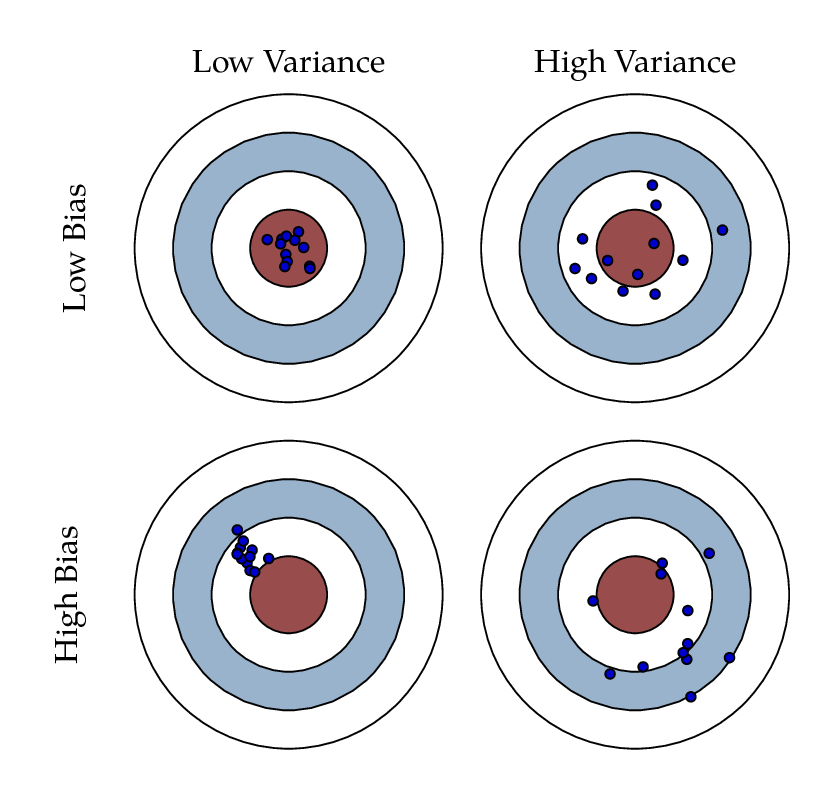
Fig. 8 Compromis biais-variance¶
Pour réduire au minimum l’erreur totale d’un modèle, il faut trouver un juste équilibre entre le biais et la variance. Étant donné un ensemble d’échantillons d’entraînement, \(x_{1}, \dots, x_{n}\), et leurs variables réponse, \(y_{1}, \dots, y_{n}\), nous voulons trouver une fonction de régression \(\hat{y}(x)\) qui estime la relation réelle \(y(x)\) aussi correctement que possible. Nous mesurons l’erreur d’estimation, c’est-à-dire la qualité (ou la mauvaise qualité) du modèle de régression, en erreur quadratique moyenne (MSE) :
La fonction de perte \(L\left(y, f_{\hat{w}}(x)\right)\) pour un modèle de régression est la différence d’erreur au carré entre les valeurs réelles et prédites, qui est \(\left(y-f_{\hat{w}_{\text {train }}}(x)\right)^{2}\)
Nous désignerons la fonction de perte comme étant l’erreur de train prévue et pour convenience nous représenterons \(f_{w_{\text {true }}}(x)\) comme \(f\) , et \(f_{\hat{w}_{t r a i n}}(x)\) comme \(\hat{f}\) Notez également que \((y-f)^{2}\) est l’erreur irréductible \(\epsilon^{2}\) et que \(\epsilon\) a une moyenne nulle impliquant \(E[\epsilon]=0\)
La fonction de perte peut maintenant s’écrire
\(\begin{aligned} L\left(y, f_{\hat{w}}(x)\right) &=E_{t r a i n}\left[\left(y-f_{w_{t r u e}}(x)+f_{w_{t r u e}}(x)-f_{\hat{w}_{t r a i n}}(x)\right)^{2}\right] \\ &=E_{t r a i n}\left[(y-f)^{2}\right]+2 E_{t r a i n}[(y-f)(f-\hat{f})]+E_{t r a i n}\left[(f-\hat{f})^{2}\right] \\ &=\epsilon^{2}+2[E[\epsilon] \times E[f-\hat{f}]+M S E(\hat{f})\\ &=\epsilon^{2}+M S E(\hat{f}) \end{aligned}\)
On peut noter que \(f_{\bar{w}}(x)\) est la moyenne des ensembles d’entraînement et est représenté par \(\bar{f}\). C’est également la valeur espérée de l’ajustement sur un ensemble d’entraînement spécifique et donc, \(\bar{f}=E_{\text {train }}[\hat{f}]\)
Par définition du biais, \([\text {Biais}(\hat{f})]^{2}=(f-\bar{f})^{2}\).
\(E_{\text{train}}[\bar{f}-\hat{f}]=\bar{f}-E_{\text {train }}[\hat{f}]=0\) et par la définition de la variance, \({Var}(\hat{f})=E\left[(\hat{f}-\bar{f})^{2}\right]\)
Décomposons maintenant \(\text{MSE}(\hat{f})\) en biais et variance
L’erreur de prédiction attendue peut maintenant s’écrire comme $\( \begin{aligned} L\left(y, f_{\hat{w}}(x)\right) &=\epsilon^{2}+M S E(\hat{f}) \\\ &=\epsilon^{2}+[\operatorname{Bias}(\hat{f})]^{2}+\operatorname{Var}(\hat{f}) \end{aligned} \)$
En résumé, le terme Biais mesure l’erreur des estimations et le terme Variance décrit la mesure dans laquelle l’estimation, \(\hat{f}\), se situe autour de sa moyenne, \(\bar{f}\). Plus le modèle d’apprentissage \(\hat{f}\) est complexe, et plus la taille des échantillons de formation est importante, plus le biais sera faible. Cependant, cela créera également un décalage plus important du modèle afin de mieux s’adapter à l’augmentation des données. Par conséquent, la variance sera levée.
- CBHK02
Nitesh V Chawla, Kevin W Bowyer, Lawrence O Hall, and W Philip Kegelmeyer. Smote: synthetic minority over-sampling technique. Journal of artificial intelligence research, 16:321–357, 2002.