Nettoyage des données¶
Le nettoyage de vos données n’est pas la tâche la plus intéressante, mais c’est une partie essentielle dans votre processus d’analyse de données. Cette tâche peut devenir très difficile, surtout lorsqu’on n’a pas une bonne connaissance du domaine de recherche ou d’étude. Il est nécessaire de bien comprendre tout le contexte qui tourne autour de vos données afin d’éviter de faire des erreurs qui peuvent causer la perte d’information.
“Garbage in, garbage out” est le principe fondamental de l’analyse des données. Le travail qui permet d’obtenir des données propres et analysables à partir des données brutes peut être long. De nombreux problèmes peuvent surgir lors du nettoyage des données en vue de leur analyse. Dans cette section, nous abordons l’identification des artefacts de traitement et l’intégration de divers ensembles de données. Nous nous concentrons ici sur le traitement avant de faire notre véritable analyse.
Gardez une copie
Il est très conseiller de toujours faire votre nettoyage des données sur une copie des données des données originales, idéalement par un pipeline qui apporte des modifications de manière systématique et répétable
Erreurs vs artéfacts¶
Les erreurs de données représentent des informations qui sont perdues lors de l’acquisition. Par exemple, des données manquantes lorsqu’un serveur tombe en panne sans backup : il s’agit là d’informations qui ne peuvent pas être reconstituées.
En revanche, les artéfacts sont généralement des problèmes systématiques résultant de la transformation des informations brutes à partir desquelles elles ont été construites. La bonne nouvelle est que les artéfacts de traitement peuvent être corrigés, tant que l’ensemble des données brutes d’origine reste disponible. La mauvaise nouvelle est que ces artéfacts doivent être détectés avant de pouvoir être corrigés.
La clé de la détection des artéfacts de traitement est de se dire; “il ya anguille sous roche”. Une mauvaise chose est généralement quelque chose d’inattendu ou de surprenant, car les gens sont naturellement optimistes. Les observations surprenantes sont la raison d’être des scientifiques. En effet, de telles observations sont la raison principale pour la science existe.
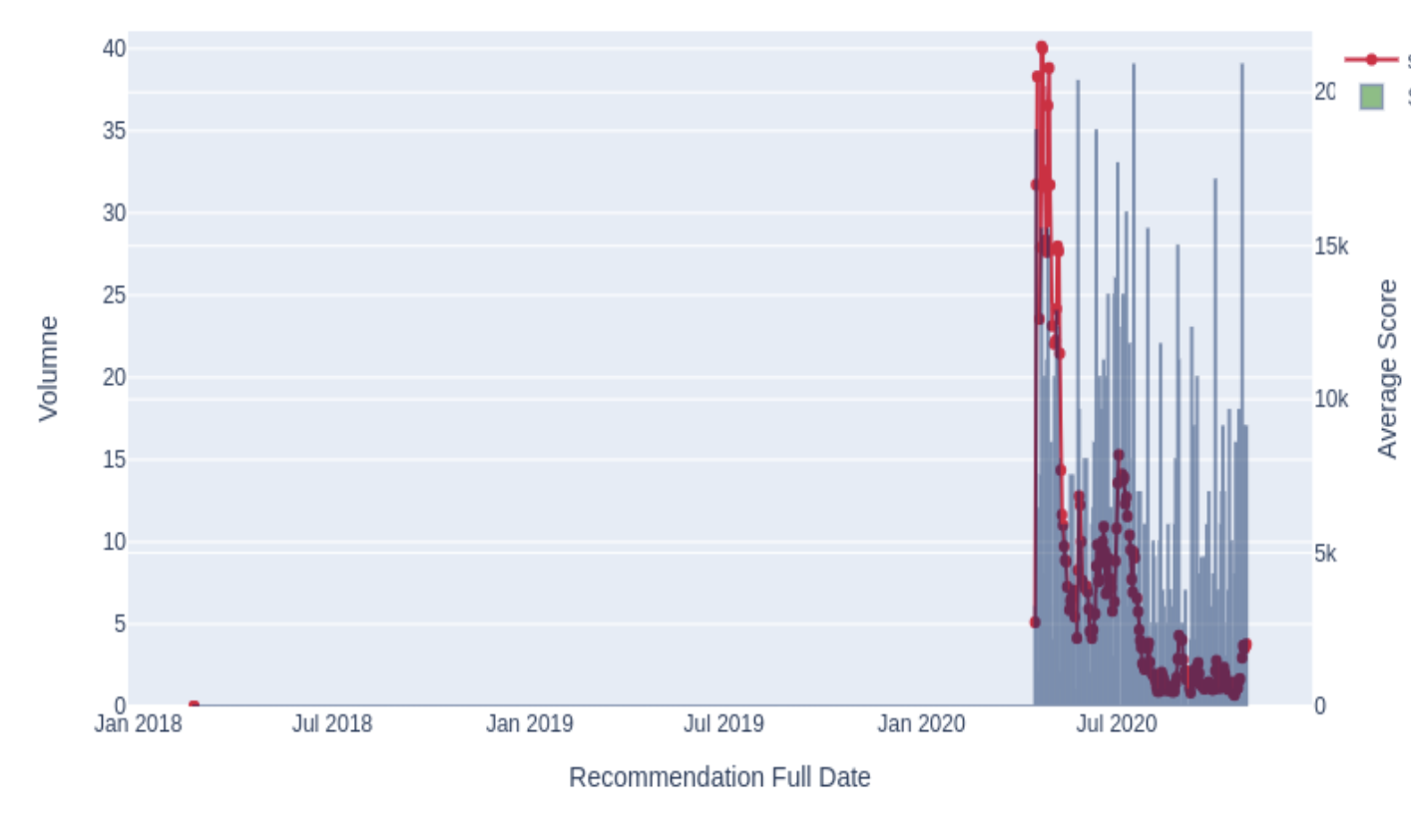
Fig. 2 Risque d’anomalie dans les transaction d’importation des produit alimetaires¶
Dans la figure (Fig. 2), on a analysé le volume (axe des y) d’import d’un certain produit dans le temps (axe des x). Le but est de l’exercice est l’analyser la fraude dans les transactions d’import de produit alimentaire. On a alors appliqué un modèle de détection d’anomalie dans le temps. À première vue, on peut voir un soudain pic de score d’anomalie (ligne rouge) à une période donnée dans le temps. Toutefois, lorsque l’on analyse de plus près nos données, on remarque que ce n’est pas vraiment une anomalie, mais il s’agit seulement d’un changement du volume d’importation (histogramme gris).
Lorsqu’on pousse un peu plus loin notre analyse, et on regarde de plus près un autre graphique (figure Fig. 3) où les couleurs représentent les différents importateurs, on voit que cette pseudoanomalie est strictement liée à un seul importateur qui importe un nouveau produit à partir d’un pays donné (où il n’existait pas d’importation précédente auparavant), et ce, c’est suite à un nouvel accord entre le Canada et ce pays.
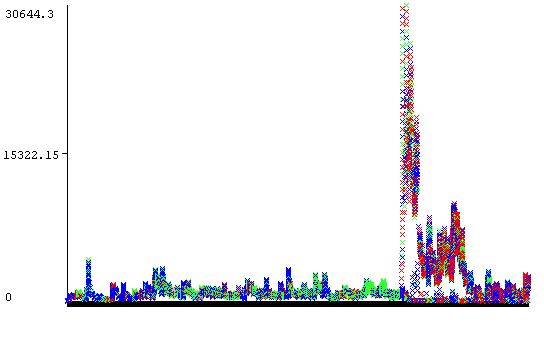
Fig. 3 Exemple d’artéfact dans des données de transactions d’import où l’on essaie de détecter les faudes d’importation¶
Compatibilité des données¶
Il arrive souvent que nous voulions fusionner des données afin d’augmeneter le nombre de variables, et ainsi augment les chances d’avoir des variables significatives afin d’enrichir la capacité de prédictions de nos modèls. Toutefois, il faut faire attention à la fusion des données faites à l’aveuglette. En effet, cela peut poser un vrai problème de compatibilité des données. Regardons quelques exemples;
Conversion des unités¶
On voit souvent des variables exprimées dans des unités différentes. Dans notre exemple des imports (figure Fig. 3)), on devait convertir la variable des prix par unité en une seule monnaie, nous avons utilisé le dollar américain au taux du jour de la transaction afin d’uniformiser cette variable peu importe de quel pays est effectué la transaction.
La conversion n’est pas toujours la solution au problème. On peut remarquer par exemple que nous avons une variable appelée quantité dans laquelle on trouve la quantité des produits importés dans une transaction, certains produits sont en kg, d’autres en grammes et même en boîte. On peut penser de convertir le tout en une seule unité (par exemple kg), mais que fait-on avec les produits très légers, mais volumineux qui sont souvent exprimés en nombre (de boîtes par exemple) ? Que fait-on avec les produits qui sont exprimés en grammes qu’ils valent assez chers (par exemple le safran)… etc. Toutes ces questions doivent être réfléchies avant de s’engager dans la modélisation de vos données qui semble bien propre.
Lors de la fusion des données provenant de sources diverses, il est recommandé de créer une nouvelle variable “origine” ou “source” pour identifier la source de provenance de chaque observation. Cela permet au moins faire des erreurs de conversion d’unités, et qui pourront être corrigée ultérieurement, en modifiant systématiquement les observations provenant de la source problématique.
Une pratique assez simple afin de détecter ces problèmes c’est de faire tests statistiques sur les données, par exemple un p-value.
Conversion numériques¶
Les variables numériques sont les plus faciles à intégrer dans les modèles mathématiques. En effet, certains algorithmes d’apprentissage machine tels que la régression linéaire et les svm ne fonctionnent qu’avec des données codées numériquement. Mais même la transformation de chiffres en nombres peut être un problème. Les variables numériques peuvent être représentés de différentes manières : sous forme d’entiers (123), de décimaux (123,5), ou même de fractions (123 1/2). Les nombres peuvent même être représentés sous forme de texte, ce qui nécessite la conversion de “dix millions” en 10000 pour le traitement numérique.
Les quantités mesurées physiquement ne sont jamais quantifiées avec précision, car nous vivons dans un monde continu. C’est pourquoi tous les biens doivent être raportés en tant que nombres réels. Des approximations entières de nombres réels sont parfois utilisées dans une tentative de gagner de l’espace. Ne faites pas cela : les effets de quantification des arrondis ou des troncatures introduisent des artefacts.
Harmonisation des noms¶
La fusion de deux ensembles de données distincts exige qu’ils partagent une même variable (la clé 🔑). Les noms sont fréquemment utilisés comme champs clés, mais ils sont souvent écrits de manière incohérente. Pensez seulement aux noms et prénoms. Pour celà on doit toujours utilisé des valeurs aplha-numérique harmonisées en encodage UTF-8 qui utilise des nombres variables de blocs de 8 bits, qui est rétrocompatible avec l’ancie encodage ASCII.
Harmonisation de l’heure et de la date¶
Les données/heures sont utilisées pour déduire l’ordre relatif des événements et regrouper les événements par simultanéité relative. L’intégration de données d’événements provenant de sources multiples nécessite un nettoyage minutieux pour garantir des résultats significatifs.
De mon expérience, je peux vous dire que les données heure/date sont les plus cauchemardesques qu’un modélisateur doit traîter. Il y a d’abord des problèmes de fuseau horaire lorsque l’on traite des données provenant de différentes régions, ainsi que la diversité des règles locales régissant les changements d’heure. La bonne solution consiste à aligner toutes les mesures de temps sur le temps universel coordonné Coordinated Universal Time (UCT), une norme moderne remplaçant le traditionnel temps moyen de Greenwich (GMT). Une norme connexe est l’heure UNIX, qui indique l’heure précise d’un événement en termes de nombre de secondes écoulées depuis 00:00:00 UTC le jeudi 1er janvier 1970.
Le calendrier grégorien est commun dans le monde de la technologie, bien que de nombreux autres systèmes de calendrier soient utilisés dans différents pays.
Les marchés financiers sont fermés les week-ends et les jours fériés, ce qui pose des problèmes d’interprétation lorsqu’il s’agit de corréler, par exemple, les cours des actions à la température locale. Quel est le bon moment du week-end pour mesurer la température, de manière à être cohérent avec les autres jours de la semaine ? Des langages comme Python contiennent de vastes bibliothèques (pandas par exemple pandas) permettant de traiter des données de séries chronologiques financières afin de résoudre ce genre de problèmes.
Harmonisation des données financières¶
L’expression “l’argent sale” est parfaitement visible dans les données financières (petit jeu de mot). En effet, la conversion des devises, qui représente les prix internationaux à l’aide d’une unité financière normalisée peut être problématique. Les taux de change peuvent varier de quelques pour cent au cours d’une journée donnée, c’est pourquoi certaines applications nécessitent des conversions sensibles au temps. Les taux de conversion ne sont pas vraiment normalisés. Les différents marchés auront chacun des taux et des écarts différents, l’écart entre les prix d’achat et le prix de vente qui couvre le coût de la conversion sont aussi différents.
L’autre correction importante concerne l’inflation. La valeur temporelle de l’argent implique qu’un dollar aujourd’hui a (généralement) différent d’un dollar dans un an, les taux d’intérêt nous permettent d’actualiser les dollars futurs. Les taux d’inflation sont estimés en suivant l’évolution des prix d’un panier d’articles, et permettent de normaliser le pouvoir d’achat d’un dollar dans le temps.
En fait, la façon la plus significative de représenter les changements de prix dans le temps n’est probablement pas les différences mais les rendements, qui normalisent la différence par le prix :
Cela s’apparente davantage à une variation en pourcentage, avec l’avantage ici que la prise du log de cette division devient symétrique aux gains et aux pertes.
Les valeurs manquantes¶
Les ensembles de données numériques supposent une valeur pour chaque élément d’une matrice. Il est tentant de fixer les valeurs manquantes à zéro, mais c’est généralement une erreur, car il y a toujours une certaine ambiguïté quant à savoir si ces valeurs doivent être interprétées comme des données ou non.
Supposons dans la variable Salaire dans une base de donnée quelconque, certaines observations sont nuls. Est-ce parce que les salariés sont au chômage, ou n’a-t-il tout simplement pas répondu à la question ?
Le danger d’utiliser des valeurs absurdes au lieu des valeurs nuls est qu’elles peuvent être mal interprétées. Un modèle de régression linéaire ajusté pour prédire les salaires en fonction de l’âge, de l’éducation et du sexe sera difficile à interpréter avec des valeurs manuantes.
Alors comment traiter les valeurs manquantes ? L’approche la plus simple consiste à supprimer toutes les observations contenant des valeurs manquantes. Cela fonctionne très bien lorsqu’il reste suffisamment de données d’entraînement, à condition que les valeurs manquantes soient absentes pour des raisons non systématiques. Par exemple, si les personnes qui refusent de déclarer leur salaire sont généralement celles qui se situent au-dessus de la moyenne, la suppression de ces observations entraînera des résultats biaisés.
Mais en général, nous voulons utiliser des observations dont les champs sont manquants. Il peut être préférable d’estimer ou d’imputer les valeurs manquantes, au lieu de les laisser nuls. Nous avons besoin de méthodes générales pour compléter ces valeurs manquantes.
L’imputation basée sur le GBS 😀 :¶
Si nous avons une connaissance suffisante du domaine, nous devrions être en mesure de faire une estimation raisonnable de la valeur de certains champs. Si je dois remplir une valeur pour l’année de votre décès, deviner l’année de naissance + 80 s’avérera à peu près correct en moyenne.
Imputation de la valeur moyenne :¶
Il est généralement judicieux d’utiliser la valeur moyenne d’une variable comme approximation des valeurs manquantes. Tout d’abord, l’ajout de valeurs supplémentaires à la moyenne laisse celle-ci inchangée, de sorte que nous ne biaisons pas nos statistiques par une telle imputation.
Mais la moyenne peut ne pas être appropriée s’il existe une raison systématique pour laquelle les données sont manquantes.
Imputation de la valeur aléatoire :¶
Une autre approche consiste à tirer une valeur aléatoire dans la variable en question afin de remplacer la valeur manquante. Cela semble nous préparer à des suppositions potentiellement mauvaises, mais c’est bien là le problème. La sélection répétée de valeurs aléatoires permet une évaluation statistique de l’impact de l’imputation. Si nous ajustons le modèle dix fois avec dix valeurs imputées différentes et obtenons des résultats très variables, alors nous ne devrions probablement continuer avec cette approche. Cette vérification de la précision est particulièrement utile lorsqu’il manque une fraction importante de valeurs dans l’ensemble des données.
Imputation par le plus proche voisin :¶
Que se passe-t-il si nous sommes capables d’identifier toutes les observations semblables (non manquantes)? Nous pouvons utiliser la technique du plus proche voisin pour déduire les valeurs de ce qui manque. Ces prédictions devraient être plus précises que la moyenne, lorsqu’il existe des raisons systématiques d’expliquer les écarts entre les observations. Cette approche nécessite une fonction de distance que nous verrons dans un peu plus tard dans le cours
Imputation par interpolation :¶
On peut utiliser une méthode comme la régression linéaire pour prédire les valeurs la variable cible. De tels modèles peuvent être entraînés sur des observations non manquante, puis appliqués à ceux dont les valeurs sont manquantes. L’utilisation de la régression linéaire pour prédire les valeurs manquantes fonctionne mieux lorsqu’il n’y a qu’un seul champ de variable manuqante par observation. Le danger potentiel ici est de créer des valeurs aberrantes significatives par des prédictions erronées. Les modèles de régression peut facilement transformer une valeur manquante en une valeur aberrante.
Les valeurs aberrantes¶
Les éléments aberrants sont souvent créés par des erreurs de saisie de données. Une vue générale des données consiste à examiner les plus grandes et les plus petites valeurs de chaque variable/colonne pour voir si elles ne sont pas trop extrêmes. Le meilleur moyen d’y parvenir est de tracer l’histogramme des fréquences et d’examiner l’emplacement des éléments extrêmes. Il est trop simple de supprimer simplement les lignes contenant des champs aberrants et de passer à autre chose. Les valeurs aberrantes indiquent souvent des problèmes plus systématiques auxquels il faut faire face.
Recherche de doublons¶
Si vous utilisez plus d’un ensemble de données avec les mêmes données brutes qui peuvent comporter des entrées en double, la suppression des doublons sera une étape importante pour garantir que vos données peuvent être mieux utilisées dans votre modèle. Si vous disposez d’un ensemble de données avec des identifiants uniques, vous pouvez utiliser ces identifiants pour vous assurer que vous n’avez pas accidentellement inséré ou acquis des données en double.
clé indexable
Si vous ne disposez pas d’un ensemble de données indexées, vous devrez peut-être trouver un bon moyen d’identifier chaque entrée unique (par exemple en créant une clé indexable).
Tout dépend des données que vous possédez, une clé unique peut ne pas être évidente. Les dates de naissance et les adresses peuvent être une bonne combinaison. Les chances que deux femmes de 24 ans se trouvent à la même adresse avec exactement la même date de naissance sont minces, même s’il n’est pas exclu qu’il s’agisse de jumelles qui vivent ensemble!
