Python; cours accéléré¶
Il existe de nombreux langages de programmation (R, MATLAB, SAS, Java, C/C++, Julia …etc.), alors pourquoi Python est si populaire ces dernières années? Python est un langage de programmation de haut niveau et polyvalent qui est utilisé dans un large éventail de domaines. Sur le site de Python, nous retrouvons un bref résumé de ce langage.
Python is an interpreted, object-oriented, high-level programming language with dynamic semantics. Its high-level built in data structures, combined with dynamic typing and dynamic binding, make it very attractive for Rapid Application Development, as well as for use as a scripting or glue language to connect existing components together. Python’s simple, easy to learn syntax emphasizes readability and therefore reduces the cost of program maintenance. Python supports modules and packages, which encourages program modularity and code reuse. The Python interpreter and the extensive standard library are available in source or binary form without charge for all major platforms, and can be freely distributed.
Ceci décrit assez bien pourquoi il est devenu si populaire aujourd’hui. En effet, il est utilisé aussi bien par les programmeurs débutants que par les développeurs experts dans plusieurs domaines techniques, scientifique ou académique.
L’écosystème du python¶
Une caractéristique majeure de Python en tant qu’écosystème, par rapport au simple fait d’être un langage de programmation, est la disponibilité d’un grand nombre de librairies. Ces dernières doivent généralement être importés lorsque cela est nécessaire (par exemple, une bibliothèque pour les graphiques). Importer signifie mettre un paquet à la disposition de l’espace de noms actuel et du processus d’interprétation Python actuel, comme nous l’avons déjà vu en R dans le cours ACT3035.
Types de données de base¶
Dans cette section, nous allons passer en revue les types de données simples en Python. Ce sont quelques-uns des éléments de base essentiels pour le traitement de l’information en Python. Les types de données que nous apprendrons sont les nombres entiers, les nombres décimaux, le Booléen, les chaînes de caractères.
Il y a un dicton qui dit que
everything in Python is an object.
En effet, Python est un language de programmation orienté objet (OOP).
Integers¶
L’un des types de données les plus fondamentaux en Python est le nombre entier, ou int :
a=10
a
10
type(a)
int
a.bit_length()
4
googol = 10 ** 100
googol.bit_length()
333
Les opérations arithmétiques sur les nombres entiers sont également faciles:
1+5
6
1/4
0.25
type(1/4)
float
L’ajout d’un point à une valeur entière, comme dans 1. ou 1.0, fait que Python interprète l’objet comme une valeur décimale.
1.9/4
0.475
type(1.9/4)
float
Booleans¶
L’évaluation d’une comparaison ou d’une expression logique (telle que 4 > 3, 4.5 <= 3.25 ou (4 > 3) et (3 > 2)) donne un True ou un False comme résultat, deux mots-clés Python.
import keyword
keyword.kwlist
['False',
'None',
'True',
'and',
'as',
'assert',
'async',
'await',
'break',
'class',
'continue',
'def',
'del',
'elif',
'else',
'except',
'finally',
'for',
'from',
'global',
'if',
'import',
'in',
'is',
'lambda',
'nonlocal',
'not',
'or',
'pass',
'raise',
'return',
'try',
'while',
'with',
'yield']
4 >= 3
True
4 == 3
False
4 != 3
True
True and True
True
True and False
False
False and False
False
not True
False
(4 > 3) and (2 > 3)
False
(not (4 != 4)) and (2 == 3)
False
int(True)
1
Strings¶
cours="vous êtes dans le cours ACT6100"
cours.capitalize()
'Vous êtes dans le cours act6100'
Conteneurs de données¶
Dans cette section, nous expliquerons les conteneurs de données, qui contiennent plusieurs points de données. Il convient toutefois de noter que ces conteneurs sont également des types de données. Python a quelques conteneurs communs : des variables, des listes et des dictionnaires.
Tuples¶
t=("ACT", 6, 100)
type(t)
tuple
t="ACT", 6, 100
type(t)
tuple
t[0]
'ACT'
t.count("ACT")
1
t.index(100)
2
Lists¶
l=["ACT", 6, 100]
type(l)
list
list(t)
['ACT', 6, 100]
type(list(t))
list
Ajoutez l’objet de la liste à la fin.¶
l.append([4,3])
l
['ACT', 6, 100, [4, 3]]
Ajoutez des éléments de l’objet liste¶
import math
l.extend([13.0, 3.14, math.pi])
l
['ACT', 6, 100, [4, 3], 13.0, 3.14, 3.141592653589793]
l.insert(5, 'Tesla')
l
['ACT', 6, 100, [4, 3], 13.0, 'Tesla', 3.14, 3.141592653589793]
l.remove("Tesla")
l
['ACT', 6, 100, [4, 3], 13.0, 3.14, 3.141592653589793]
len(l)
7
Structure de contrôl¶
Ici nous intégrons un exemple sur les boucles for et les condition if. Une boucle est un moyen d’itération sur des objets Python, couramment utilisés avec des listes. Une boucle for loop indique : “Pour chaque chose de cette liste de choses, faites quelque chose”. Le premier mot utilisé après for est la variable qui va contenir chaque objet de la liste (ou autre objet itérable). Le code situé sous la boucle for utilise cette variable pour effectuer d’autres fonctions ou calculs sur l’objet.
for element in l[4:7]:
print(element ** 2)
169.0
9.8596
9.869604401089358
for i in range(1, 10) :
if i % 2 == 0 :
print("%d est pair" % i)
elif i % 3 == 0 :
print("%d est un multiple de 3" % i)
else :
print("%d is impair" % i)
1 is impair
2 est pair
3 est un multiple de 3
4 est pair
5 is impair
6 est pair
7 is impair
8 est pair
9 est un multiple de 3
Les fonctions¶
Une fonction est un bloc de code organisé et réutilisable qui est utilisé pour effectuer une action quelconque. Les fonctions offrent une meilleure modularité qui peut être réutilisable dans votre code.
def pair(x):
return x%2==0
pair(3)
False
list(map(pair, range(10)))
[True, False, True, False, True, False, True, False, True, False]
Les fonctions peuvent également être utilisées pour filtrer un objet de la liste. Dans l’exemple suivant, le filtre renvoie les éléments d’un objet de liste qui correspondent à la condition booléenne telle que définie par la fonction pair :
list(filter(pair, range(15)))
[0, 2, 4, 6, 8, 10, 12, 14]
Dictionnaire¶
Les objets dict sont des dictionnaires, mais aussi des séquences mutables, qui permettent de récupérer des données par des clés (qui peuvent, par exemple, être des objets str). Ce sont ce qu’on appelle des “key-value stores”. Alors que les objets de liste sont ordonnés et triables, les objets dict sont en général non ordonnés et non triables.
d={
"Nom" : "François Legault",
"Voiture_mrq": "Honda",
"Voiture_mdl": "Civic",
"Profession":"Premier ministre",
"Âge" : 64
}
type(d)
dict
print(d['Nom'], d['Âge'])
François Legault 64
d.keys()
dict_keys(['Nom', 'Voiture_mrq', 'Voiture_mdl', 'Profession', 'Âge'])
d.values()
dict_values(['François Legault', 'Honda', 'Civic', 'Premier ministre', 64])
d.items()
dict_items([('Nom', 'François Legault'), ('Voiture_mrq', 'Honda'), ('Voiture_mdl', 'Civic'), ('Profession', 'Premier ministre'), ('Âge', 64)])
for item in d.items():
print(item)
('Nom', 'François Legault')
('Voiture_mrq', 'Honda')
('Voiture_mdl', 'Civic')
('Profession', 'Premier ministre')
('Âge', 64)
d['Âge'] += 1
for item in d.items():
print(item)
('Nom', 'François Legault')
('Voiture_mrq', 'Honda')
('Voiture_mdl', 'Civic')
('Profession', 'Premier ministre')
('Âge', 65)
Numpy¶
numpy.ndarray est une classe construite dans le but spécifique de manipuler des tableaux de \(n\)-dimensions de manière pratique et efficace.
import numpy as np
a = np.array([0, 1/2, 1, 3/2, 2])
a.sum()
5.0
a.std()
0.7071067811865476
a.cumsum()
array([0. , 0.5, 1.5, 3. , 5. ])
a**2
array([0. , 0.25, 1. , 2.25, 4. ])
2**a
array([1. , 1.41421356, 2. , 2.82842712, 4. ])
np.exp(a)
array([1. , 1.64872127, 2.71828183, 4.48168907, 7.3890561 ])
b = np.array([a, a * 2])
b
array([[0. , 0.5, 1. , 1.5, 2. ],
[0. , 1. , 2. , 3. , 4. ]])
b[0, 2]
1.0
b[:, 1]
array([0.5, 1. ])
b.sum()
15.0
b.sum(axis=0)
array([0. , 1.5, 3. , 4.5, 6. ])
b.sum(axis=1)
array([ 5., 10.])
g = np.arange(15)
g.shape
(15,)
g.reshape((3, 5))
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
h = g.reshape((5, 3))
h
array([[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11],
[12, 13, 14]])
h.T
array([[ 0, 3, 6, 9, 12],
[ 1, 4, 7, 10, 13],
[ 2, 5, 8, 11, 14]])
h.transpose()
array([[ 0, 3, 6, 9, 12],
[ 1, 4, 7, 10, 13],
[ 2, 5, 8, 11, 14]])
Pandas¶
Le DataFrame est une classe conçue pour traiter efficacement les données sous forme de tableaux, c’est-à-dire les données caractérisées par une organisation en colonnes. À cette fin, la classe DataFrame fournit, par exemple, un étiquetage des colonnes ainsi que des capacités d’indexation flexibles pour les lignes (opbservations) de l’ensemble de données, comme un tableau dans une base de données relationnelle ou une feuille de calcul Excel.
import pandas as pd
pi=math.pi
pi
3.141592653589793
df = pd.DataFrame([pi, pi/2, pi*2, pi**2],
columns=['pi'],
index=['a', 'b', 'c', 'd'])
df
| pi | |
|---|---|
| a | 3.141593 |
| b | 1.570796 |
| c | 6.283185 |
| d | 9.869604 |
df.index
Index(['a', 'b', 'c', 'd'], dtype='object')
df.columns
Index(['pi'], dtype='object')
df.loc['c']
pi 6.283185
Name: c, dtype: float64
df.loc[['a', 'd']]
| pi | |
|---|---|
| a | 3.141593 |
| d | 9.869604 |
df.iloc[1:3]
| pi | |
|---|---|
| b | 1.570796 |
| c | 6.283185 |
df.sum()
pi 20.865179
dtype: float64
df.apply(lambda x: x ** 2)
| pi | |
|---|---|
| a | 9.869604 |
| b | 2.467401 |
| c | 39.478418 |
| d | 97.409091 |
df**2
| pi | |
|---|---|
| a | 9.869604 |
| b | 2.467401 |
| c | 39.478418 |
| d | 97.409091 |
df['floats'] = (1.5, 2.5, 3.5, 4.5)
df
| pi | floats | |
|---|---|---|
| a | 3.141593 | 1.5 |
| b | 1.570796 | 2.5 |
| c | 6.283185 | 3.5 |
| d | 9.869604 | 4.5 |
df.describe()
| pi | floats | |
|---|---|---|
| count | 4.000000 | 4.000000 |
| mean | 5.216295 | 3.000000 |
| std | 3.669041 | 1.290994 |
| min | 1.570796 | 1.500000 |
| 25% | 2.748894 | 2.250000 |
| 50% | 4.712389 | 3.000000 |
| 75% | 7.179790 | 3.750000 |
| max | 9.869604 | 4.500000 |
df.mean()
pi 5.216295
floats 3.000000
dtype: float64
df.mean(axis=0)
pi 5.216295
floats 3.000000
dtype: float64
df.mean(axis=1)
a 2.320796
b 2.035398
c 4.891593
d 7.184802
dtype: float64
df.cumsum()
| pi | floats | |
|---|---|---|
| a | 3.141593 | 1.5 |
| b | 4.712389 | 4.0 |
| c | 10.995574 | 7.5 |
| d | 20.865179 | 12.0 |
Visualization¶
At their best, graphics are instruments for reasoning.
– Edward Tufte
La visualisation efficace des données est un aspect important de la science des données, pour au moins trois raisons distinctes :
Analyse exploratoire des données: Ici, on veut avoir un apperçu sur nos données..
Analyse des modèles et leur performance: Ici, on cherche à avoir un apperçu de notre modèle, on cherche à détecter les possibles erreurs.
La communication: Une fois nos modèles sont validés, on veut les communiquer et/ou les partager.
from pylab import plt, mpl
plt.style.use('seaborn')
mpl.rcParams['font.family'] = 'serif'
%matplotlib inline
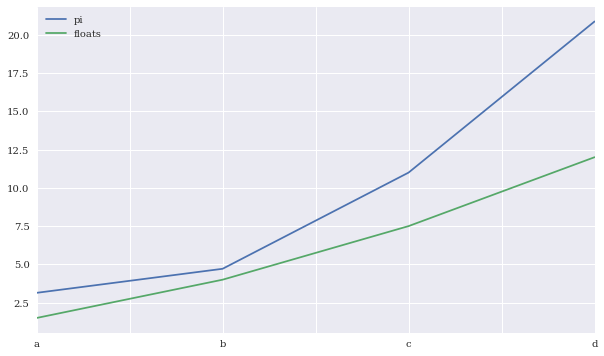
df.cumsum().plot(figsize=(10, 6));
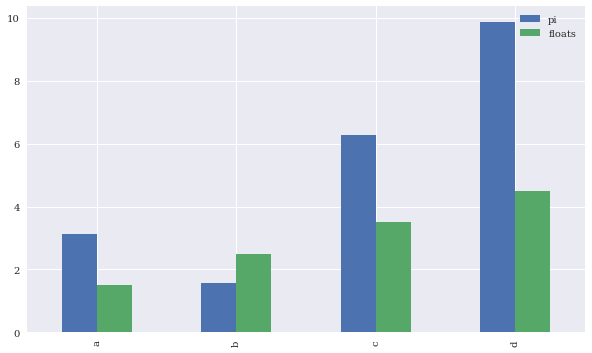
df.plot.bar(figsize=(10, 6));
Group et concat¶
Cette matière a déjà été vue dans le cours ACT3035 sous le chapitre dplyr de R. C’est exactement la même chose!
Vecteurs et Matrices¶
De manière abstraite, les vecteurs sont des objets qui peuvent être additionnés ensemble (pour former de nouveaux vecteurs) et qui peuvent être multipliés par des scalaires (c’est-à-dire des nombres), également pour former de nouveaux vecteurs.
Concrètement (pour nous), les vecteurs sont des points dans un espace à dimension finie. Même si vous ne considérez pas vos données comme des vecteurs, elles constituent un bon moyen de représenter des données numériques.
Par exemple, si vous avez la taille, le poids et l’âge d’un grand nombre de personnes, vous pouvez traiter vos données comme des vecteurs tridimensionnels (taille, poids, âge). Si l’on a quatre examens dans le cours ACT6100 à faire, vous pouvez traiter les notes d’étudiants comme des vecteurs quadridimensionnels (examen1, examen2, examen3, examen4). L’approche la plus simple consiste à représenter les vecteurs sous forme de listes de nombres.
Calculons \(2 I+3 A-A B\) for $\( A=\left[\begin{array}{cc} 1 & 3 \\ -1 & 7 \end{array}\right] \quad B=\left[\begin{array}{ll} 5 & 2 \\ 1 & 2 \end{array}\right] \)\( où \)I$ est une matrice identité de taille 2 :
import numpy as np
import scipy.linalg as la
A = np.array([[1,3],[-1,7]])
print(A)
[[ 1 3]
[-1 7]]
B = np.array([[5,2],[1,2]])
print(B)
[[5 2]
[1 2]]
I = np.eye(2)
print(I)
[[1. 0.]
[0. 1.]]
2*I + 3*A - A@B
array([[-3., 1.],
[-5., 11.]])
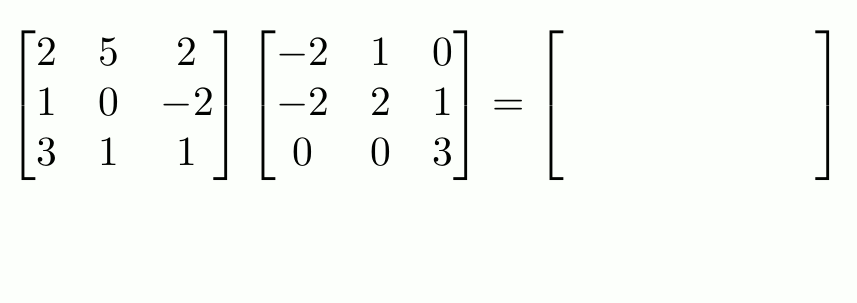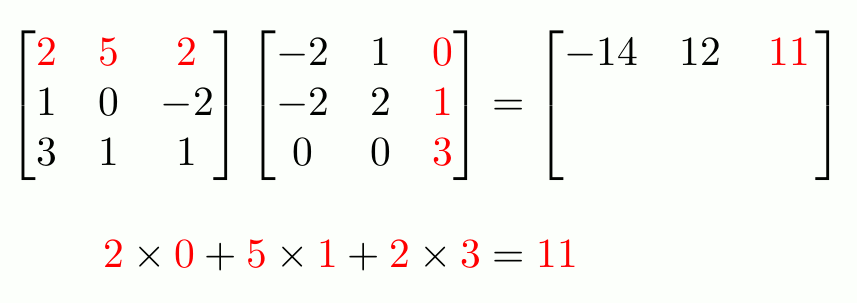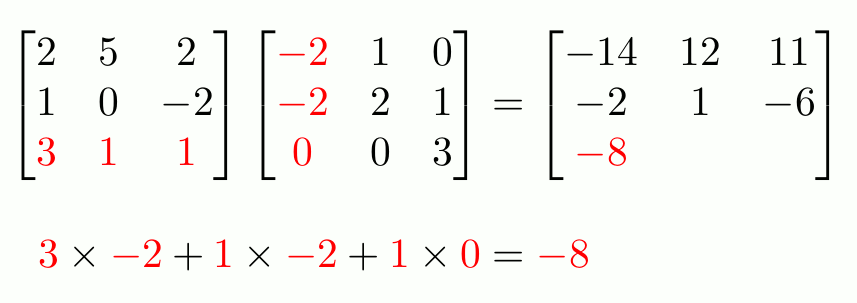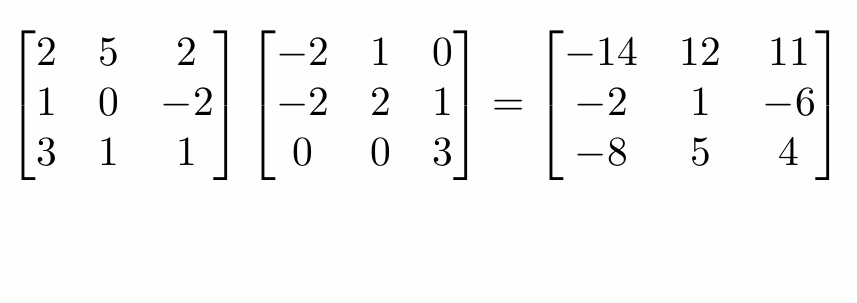
Il n’y a pas de symbole pour les puissances matricielles et nous devons donc importer la fonction matrix_power:
from numpy.linalg import matrix_power as mpow
M = np.array([[3,4],[-1,5]])
print(M)
[[ 3 4]
[-1 5]]
mpow(M,2)
array([[ 5, 32],
[-8, 21]])
mpow(M,5)
array([[-1525, 3236],
[ -809, 93]])
M @ M @ M @ M @ M
array([[-1525, 3236],
[ -809, 93]])
Transpose¶
print(M)
[[ 3 4]
[-1 5]]
print(M.T)
[[ 3 -1]
[ 4 5]]
Remarquez que \(M M^{T}\) est une matrice symétrique :
M @ M.T
array([[25, 17],
[17, 26]])
Inverse¶
print(A)
[[ 1 3]
[-1 7]]
la.inv(A)
array([[ 0.7, -0.3],
[ 0.1, 0.1]])
A linear system of equations is a collection of linear equations
In matrix notation, a linear system is \(A \mathbf{x}=\mathbf{b}\) where
N = 1000
A = np.random.rand(N,N)
b = np.random.rand(N,1)
# Regardons les premières observations
A[:4,:3]
array([[0.91430299, 0.77985506, 0.49013321],
[0.49253285, 0.92236314, 0.34642134],
[0.00162082, 0.05763338, 0.46917428],
[0.96175421, 0.66257052, 0.27640879]])
b[:4,:]
array([[0.39189543],
[0.33885905],
[0.34093499],
[0.40880476]])
x = la.solve(A,b)
x[:4,:]
array([[ 3.07023193],
[-1.13442351],
[ 0.55661619],
[ 3.32424416]])
