Robust Regression¶
Les modèles que nous avons vus jusqu’à maintenant sont, sensibles aux valeurs aberrantes. Une valeur aberrante peut être définie de plusieurs façons, mais en général, une valeur aberrante une observation dont la valeur diffère sensiblement des autres observations de l’échantillon.
Mais pourquoi les modèles linéaires sont-ils sensibles aux valeurs aberrantes ? Toutes les méthodes que nous avons utilisées jusqu’à présent minimisent une fonction objective qui est basée sur la somme résiduelle des carrés, et donc chaque point de l’ajustement contribue à cette fonction de coût objective. Pour surmonter ce problème potentiel, la régression robuste offre une alternative valable aux modèles linéaires standard, et est particulièrement suggérée lorsque nous soupçonnons la présence de valeurs aberrantes dans l’échantillon ou d’hétéroscédasticité dans le modèle. En particulier, étant donné que les valeurs aberrantes ont tendance à avoir un impact significatif sur la procédure d’estimation de l’ajustement OLS affectant la pente de la courbe d’ajustement, les modèles de régression robuste réduisent en fait l’influence des valeurs aberrantes, ce qui facilite leur détection.
Nous introduirons ici quelques méthodes permettant l’ajustement de la régression robuste, à savoir la régression de Huber et le RANdom SAmple Consensus (RANSAC), mis en place par Huber (1964) et Fischler et Bolles (1981), respectivement. Le lecteur intéressé peut se référer au livre d’Andersen (2008) pour plus de détails et les différentes méthodologies sur cette question.
Huber Regression¶
Cette méthode a été proposée par Peter Huber [Hub92] en 1964, et elle étend la MCO stadard en introduisant une perte qui est moins sensible aux valeurs aberrantes lorsque le modèle de sortie brut (c’est-à-dire la différence entre la valeur observée et la valeur prédite) est trop important. En particulier, cela est obtenu en introduisant une perte qui est une fonction par morceaux qui optimise soit la perte au carré soit la perte absolue pour les échantillons sur la base d’un paramètre, noté par ε, qui contrôle essentiellement le nombre de valeurs aberrantes ayant un impact sur l’ajustement. De manière plus formelle, nous souhaitons minimiser la fonction de coût suivante :
où $\( L(y, f(x))=\left\{\begin{array}{l} (y-f(x))^{2} \quad \text { if }|y-f(x)|<\epsilon \\ 2 \cdot \epsilon \cdot|y-f(x)| \quad \text { ailleurs } \end{array}\right. \)$
Ainsi, la fonction de perte de Huber est élevée au carrée pour les petites erreurs de prédiction, et linéaire pour les valeurs plus importantes, qui sont susceptibles de se produire lorsque des valeurs aberrantes sont observées.
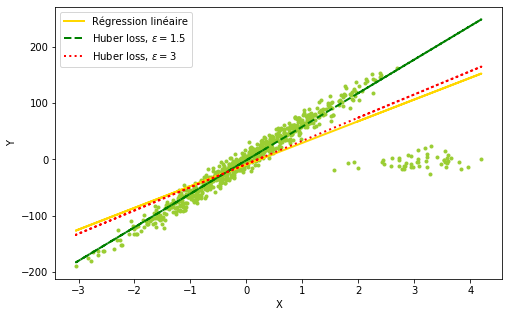
À titre d’illustration, essayons de faire tenir un modèle OLS simple sur un ensemble de données avec des valeurs aberrantes. Comme le montre la figure 2.7, le modèle estimé est tiré vers le bas par le groupe de valeurs aberrantes, indiqué dans la direction est du graphique.
Ici, nous appliquons deux fois la fonction personnalisée appelée fit_huber, qui correspond essentiellement à un régresseur Huber et renvoie le modèle de régression temporisée es-. Nous voyons, toujours à partir de la figure 2.7, qu’un ε → 1 produit un modèle qui oublie les valeurs aberrantes, là où le modèle tend à se rapprocher de l’estimateur MCO à mesure que ce paramètre augmente.
from sklearn.linear_model import LinearRegression, HuberRegressor, RANSACRegressor
from sklearn import datasets
import numpy as np
from matplotlib import pyplot as plt
plt.figure(figsize=(8,5))
plt.scatter(X,y,color='yellowgreen', marker='.')
plt.plot(X, ols, label='Régression linéaire',
color='gold', linestyle='solid', linewidth=2)
plt.plot(X, huber1, label="Huber loss, $\epsilon=1.5$",
color='green', linestyle='dashed', linewidth=2)
plt.plot(X, huber2, label="Huber loss, $\epsilon=3$",
color='red', linestyle='dotted', linewidth=2 )
plt.legend(loc='upper left')
plt.xlabel("X")
plt.ylabel("Y")
plt.show()
RANSAC¶
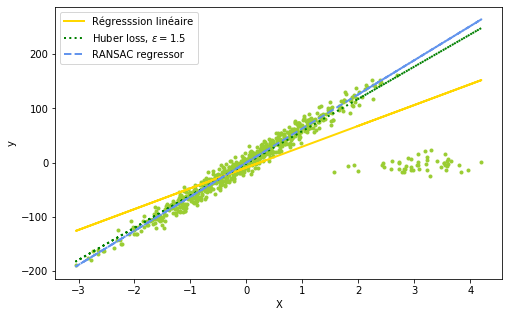
Le RANSAC n’est pas à proprement parler un modèle statistique, mais un algorithme itératif, développé en 1981, qui s’avère extrêmement cohérent par rapport aux valeurs aberrantes. Il divise essentiellement les données disponibles en deux sous-ensembles différents, à savoir les valeurs aberrantes et les valeurs non aberrantes. Ce dernier sous-ensemble est également désigné comme étant les valeurs hypothétiques des valeurs aberrantes. Les valeurs aberrantes hypothétiques sont utilisées pour ajuster le modèle, tandis que le premier groupe est ensuite utilisé pour calculer les erreurs résiduelles.
Tous les points qui s’en tiennent à la prédiction du modèle sont regroupés pour former l’ensemble de consensus. L’algorithme du RANSAC continue d’itérer jusqu’à ce que l’ensemble consensuel soit suffisamment grand pour que l’ajustement soit cohérent par rapport aux valeurs aberrantes. L’extrait suivant contient une fonction personnalisée, appelée fit_RANSAC, qui renvoie le modèle prédit : les résultats de l’ajustement sur cet ensemble de données synthétiques sont présentés à la figure 2.8.
plt.figure(figsize=(8,5))
plt.scatter(X,y,color='yellowgreen', marker='.')
plt.plot(X, ols, label='Régresssion linéaire',
color='gold', linestyle='solid', linewidth=2)
plt.plot(X, huber1, label="Huber loss, $\epsilon=1.5$", color='green',linestyle='dotted', linewidth=2)
plt.plot(X, ransac,label='RANSAC regressor', color='cornflowerblue', linestyle='dashed', linewidth=2)
plt.legend(loc='upper left')
plt.xlabel("X")
plt.ylabel("y")
plt.show()
- Hub92
Peter J Huber. Robust estimation of a location parameter. In Breakthroughs in statistics, pages 492–518. Springer, 1992.