Éviter le overfitting¶

Dans cette section, nous parlons des techniques qu’on peut utiliser afin d’éviter le surajustement, telle que la validation croisée ainsi que la régularisation et la réduction des variables pour trouver le modèle optimal en équilibrant le biais et la variance et pour diminuer l’effet du surajustement.

Validation croisée (CV)¶

Pour les grands ensembles de données, l’échantillon original de données peut être divisé en un ensemble d’entraînement sur lequel on ajuste le modèle, un ensemble de validation sur lequel on valide nos modèles et un ensemble de test pour évaluer notre modèle formé. Cependant, lorsque nous ne disposons pas de grands échantillons de données, la validation croisée est particulièrement utile. La validation croisée (CV) nous permet de sélectionner un modèle et d’estimer l’erreur dans le modèle.

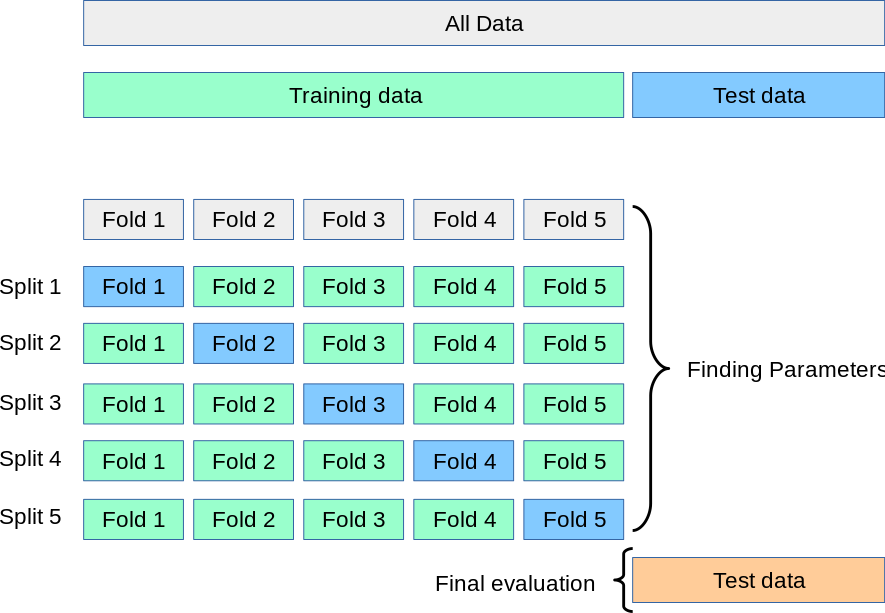
Fig. 9 Le processus de validation croisée¶

Rappelons notre examen de la SOA qu’entre les questions pratiques et les examens réels, il existe des examens fictifs qui nous permettent d’évaluer nos performances lors de l’examen réel et d’utiliser ces informations pour effectuer les révisions nécessaires. Dans l’apprentissage machine, la procédure de validation permet d’évaluer comment les modèles vont se généraliser à des ensembles de données indépendants. Dans un cadre de validation classique, les données originales sont divisées en trois sous-ensembles, généralement 60 % pour l’ensemble de formation, 20 % pour l’ensemble de validation et le reste (20 %) pour l’ensemble test. Ce paramètre est suffisant si nous disposons d’un large ensemble de données d’entraînement. Dans le cas contraire, une validation croisée est le meilleur choix.

Il y a principalement deux méthodes de validation croisée: exhaustif et non exhaustif.

LOOCV¶

Dans la méthode exhaustive, nous omettons un nombre fixe d’observations dans chaque cycle comme échantillons de test (ou de validation) et utilisons les observations restantes comme échantillons d’entraînement. Ce processus est répété jusqu’à ce que tous les différents sous-ensembles possibles d’échantillons sont utilisés une fois pour les tests. Par exemple, nous pouvons appliquer la validation croisée des échantillons sans prélèvement ( Leave-One-Out- Cross-Validation - LOOCV), qui permet à chaque échantillon de faire partie de la série de tests une fois. Pour un ensemble de données de taille \(n\), la LOOCV nécessite \(n\) cycles de validation croisée. Cela peut être lent lorsque la taille de \(n\) devient importante.

Fig. 10 Leave-One-Out- Cross-Validation - LOOCV¶

from sklearn.model_selection import LeaveOneOut

X = [1, 2, 3, 4]
loo = LeaveOneOut()
for train, test in loo.split(X):
    print("%s %s" % (train, test))

[1 2 3] [0]
[0 2 3] [1]
[0 1 3] [2]
[0 1 2] [3]

Validation croisée k-fold¶

La méthode non exhaustive, en revanche, comme son nom l’indique, n’essaie pas toutes les partitions possibles. Le type le plus utilisé de ce schéma est la validation croisée k-fold. Nous commençons par diviser aléatoirement les données d’origine en partitions de taille égale. Dans chaque essai, une de ces partitions devient l’ensemble de test, et le reste des données devient l’ensemble d’entraînement.

import numpy as np
from sklearn.model_selection import KFold

X = [1, 2, 3, 4]
kf = KFold(n_splits=2)
for train, test in kf.split(X):
    print("%s %s" % (train, test))

On voit bien dans la figure ci-dessous que la validation croisée k-fold n’est pas affectée par des classes ou des groupes.

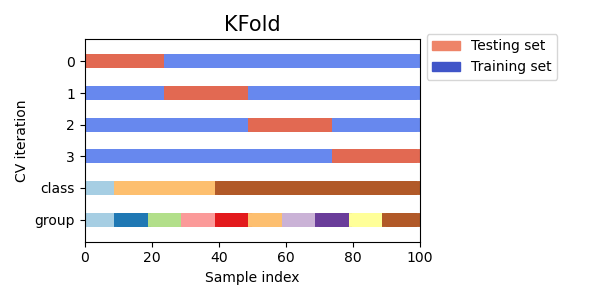
Fig. 11 KFold n’est pas affecté par des classes ou des groupes.¶

En résumé, la validation croisée permet d’obtenir une évaluation plus précise de la performance des modèles en combinant les mesures de la performance de prédiction sur différents sous-ensembles de données. Cette technique permet non seulement de réduire la variance et d’éviter le surajustement, mais elle donne également un aperçu de la façon dont le modèle se comportera généralement dans la pratique. D’ailleurs, vous pouvez voir plus de détail sur la validation croisée en Python dans la documentation de scikit_learn [sci].

Régularisation¶

Le surajustement est associé à un nombre important de paramètres (structurels) estimés. Il y a également surajustement lorsque le nombre de variables est très élevé par rapport au nombre d’observations.

Rappelons que la complexité inutile du modèle est aussi une source de surajustement. Par exemple, une régression linaire simple avec seulement deux paramètres \(Y= \beta_0 + \beta_1 X \) où \(\beta_0\) et \(\beta_1\) sont deux constantes inconnues qui représentent les termes de l’intercept (\(\beta_0\)) et de la pente (\(\beta_1\) ) est le modèle le plus simple. Contrairement à cela, il est beaucoup plus facile de trouver un modèle qui capture parfaitement tous les points de données d’entraînement avec une fonction polynomiale d’ordre élevé, car son espace de recherche est beaucoup plus grand que celui d’une fonction linéaire. Cependant, ces modèles faciles à obtenir se généralisent moins bien que les modèles linéaires, qui sont plus sujets au surajustement. Et, bien sûr, les modèles plus simples nécessitent moins de temps de calcul. Le diagramme suivant montre comment nous essayons d’ajuster une fonction linéaire et une fonction polynomiale d’ordre supérieur.

La régularisation ajoute des paramètres supplémentaires à la fonction d’erreur que nous essayons de minimiser, afin de pénaliser les modèles complexes. En plus, si nous limitons le temps d’apprentissage d’un modèle ou si nous fixons certains critères d’arrêt internes, il est plus probable que nous produisions un modèle plus simple. La complexité du modèle sera ainsi contrôlée et, par conséquent, le surajustement devient moins probable. Cette approche est appelée “arrêt anticipé” ou “early stopping” dans l’apprentissage machine.

Sélection de variables et réduction de dimensions¶

Les données sont habituellement représentées sous forme de tableau (matrice), où chaque ligne représente une observation et chaque colonne représente une variable explicative (appelée des fois caractéristique). Dans l’apprentissage supervisé, une des colones est appelé la variable réponse (ou l’étiquette) que notre modèle essaiera de prédire.

Le nombre de variables (caractéristiques) correspond à la dimensionnalité des données. Notre modèle d’apprentissage machine dépend du nombre de dimensions (variables explicatives) par rapport au nombre d’observations. Par exemple, les données de texte et d’image ont une dimension très élevée, alors que les données d’assurance ont relativement moins de dimensions.

L’ajustement de données à haute dimension est coûteux en termes de calcul et est susceptible d’être surajusté en raison de la grande complexité des données. Les dimensions plus élevées sont également impossibles à visualiser, et nous ne pouvons donc pas utiliser de méthodes d’analytiques simples. Pensons seulement au modèle GPT-2 [RWC+19] qui a été entraîné simplement pour prédire le prochain mot dans un texte/phrase a nécessité près dans 40 Go de texte Internet. Ce modèle contient 1,5 milliard de paramètres, entraîné sur un ensemble de données de 8 millions de pages web.

Le successeur de ce modèle, GPT-3 a nécessité 1.75 milliard de paramètres [BMR+20] aurait coûté plus de 4,6 millions de dollars [lam] en utilisant une instance Cloud de Tesla V100.

Nous détaillerons plus cette technique un peu plus loin dans la session.

Hyperparamètres¶

Les hyperparamètres (aussi appelés paramètres de réglage) sont des paramètres du modèle utilisés pour contrôler le comportement de ce dernier. Ils permettent de contrôler la complexité des algorithmes d’apprentissage machine, par conséquent, le compromis biais-variance. La plupart des algorithmes en ont au moins un ou plusieurs hyperparamètres. Par exemple;

Le nombre de centroïdes dans un algorithme de regroupement (clustering)
Le taux d’apprentissage
Le nombre de feuilles ou la profondeur d’un arbre dans les algorithmes basés sur les arbres

En permettant à l’algorithme d’apprentissage d’itération sur une gamme de valeurs, les “meilleures” valeurs des hyperparamètres peuvent être obtenues, ce qui diminue la fonction de perte sur les données invisibles.

sci: 3.1. Cross-validation: evaluating estimator performance — scikit-learn 0.24.1 documentation. URL: https://scikit-learn.org/stable/modules/cross{\_}validation.html (visited on 2021-01-25).
lam: OpenAI’s GPT-3 Language Model: A Technical Overview. URL: https://lambdalabs.com/blog/demystifying-gpt-3/ (visited on 2021-01-26).
BMR+20: Tom B Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, and others. Language models are few-shot learners. arXiv preprint arXiv:2005.14165, 2020.
RWC+19: Alec Radford, Jeffrey Wu, Rewon Child, David Luan, Dario Amodei, and Ilya Sutskever. Language models are unsupervised multitask learners. OpenAI blog, 1(8):9, 2019.

ACT6100