Analyse par composantes principales¶
Dans cette section, nous explorons ce qui est peut-être l’un des algorithmes d’apprentissage machine le plus largement utilisés, l’analyse en composantes principales (ACP). L’ACP est fondamentalement un algorithme de réduction de la dimensionnalité, mais elle peut également être utile comme outil de visualisation, de filtrage du bruit, d’extraction et d’ingénierie de caractéristiques (feature engineering), et bien plus encore. Après une brève discussion conceptuelle de l’algorithme PCA, nous verrons quelques exemples de ces autres applications.
Introduction à l’analyse en composantes principales¶
L’analyse en composantes principales est une méthode rapide de réduction de la dimension des données. Son comportement est plus facile à visualiser en examinant un ensemble de données bidimensionnelles. Considérez les 200 points suivants :
À l’oeil nu, il est clair qu’il existe une relation presque linéaire entre les variables \(x\) et \(y\). Cela rappelle les données de régression linéaire que nous avons vu, mais le problème posé ici est légèrement différent : plutôt que d’essayer de prédire les valeurs \(y\) à partir des valeurs \(x\), le problème d’apprentissage non supervisé tente de connaître la relation entre les valeurs \(x\) et \(y\).
Dans l’analyse en composantes principales, cette relation est quantifiée en trouvant une liste des axes principaux dans les données, et en utilisant ces axes pour décrire l’ensemble de données. En utilisant l’estimateur PCA de Scikit-Learn, nous pouvons calculer cela comme suit :
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(X)
PCA(copy=True, iterated_power='auto', n_components=2, random_state=None,
svd_solver='auto', tol=0.0, whiten=False)
L’ajustement apprend certaines quantités à partir des données, surtout les “composantes” et la “variance expliquée” :
print(pca.components_)
[[-0.94446029 -0.32862557]
[-0.32862557 0.94446029]]
print(pca.explained_variance_)
[0.7625315 0.0184779]
Pour voir ce que ces nombres signifient, considérons-les comme des vecteurs sur les données d’entrée, en utilisant les “composantes” pour définir la direction du vecteur, et la “variance expliquée” pour définir la longueur au carré du vecteur :
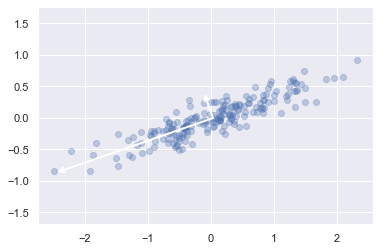
Ces vecteurs représentent les principaux axes des données, et la longueur du vecteur est une indication de l’importance de cet axe dans la description de la distribution des données - plus précisément, c’est une mesure de la variance des données lorsqu’elles sont projetées sur cet axe. La projection de chaque point de données sur les axes principaux sont les “composantes principales” des données.
Préserver la variance¶
Avant de pouvoir projeter l’ensemble de formation sur un hyperplan de dimension inférieure, vous devez d’abord choisir le bon hyperplan. Par exemple, un simple ensemble de données 2D est représenté à gauche de la figure ci-dessous, avec trois axes différents (c’est-à-dire des hyperplans unidimensionnels). À droite, on voit le résultat de la projection de l’ensemble de données sur chacun de ces axes. Comme vous pouvez le voir, la projection sur la ligne pleine préserve la variance maximale, tandis que la projection sur la ligne pointillée préserve une très faible variance, et la projection sur la ligne en tiret (au milieu) préserve une variance intermédiaire.
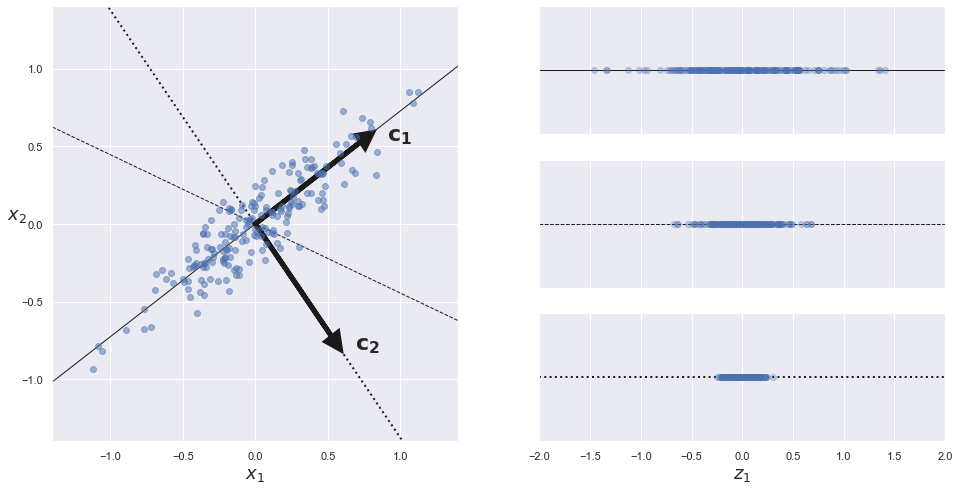
Il semble raisonnable de choisir l’axe qui préserve le maximum de variance, car il perdra très probablement moins d’informations que les autres projections. Une autre façon de justifier ce choix est que c’est l’axe qui minimise le carré moyen de la variance entre l’ensemble de données original et sa projection sur cet axe. C’est l’idée assez simple qui sous-tend l’ACP.
Composantes principales¶
L’ACP identifie l’axe qui représente la plus grande variance dans l’ensemble de l’entrainement. Dans la figure ci-dessus, il s’agit de la ligne continue. Elle trouve également un deuxième axe, orthogonal au premier, qui représente la plus grande variance restante. Dans cet exemple en 2D, ce deuxième choix c’est la ligne pointillée. S’il s’agissait d’un ensemble de données à dimensions supérieures, l’ACP trouverait également un troisième axe, orthogonal aux deux axes précédents, et un quatrième, un cinquième, et ainsi de suite, autant d’axes que le nombre de dimensions de l’ensemble de données.
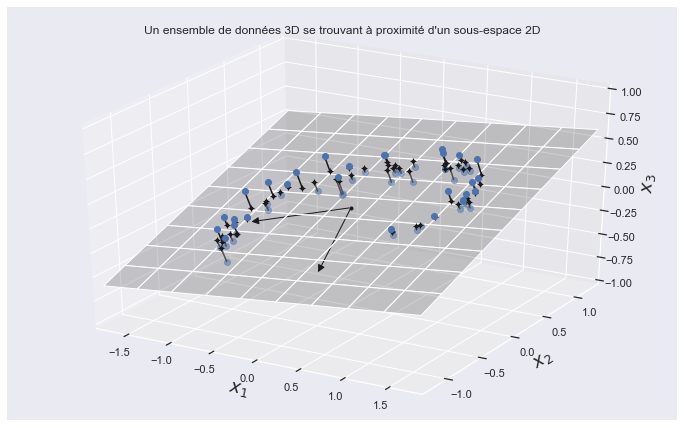
Le vecteur unitaire qui définit le ième axe est appelé la ième composante principale. Dans la figure ci-dessus, la première CP est \(c_1\) et le 2ème CP est \(c_2\). Dans la figure ci-dessous, les deux première CP sont représentés par les flèches orthogonales dans le plan, et le troisième composante serait orthogonal au plan (pointant vers le haut ou vers le bas).
Ratio de variance expliqué¶
Un autre élément d’information très utile est le rapport de variance expliqué de chaque composante de principale, disponible via la variable explained_variance_ratio_. Elle indique la proportion de la variance de l’ensemble de données qui se trouve sur l’axe de chaque composante principale. Par exemple, examinons les rapports de variance expliqués des deux premières composantes de l’ensemble de données 3D représenté sur la figure ci-dessus :
print(pca.explained_variance_ratio_)
[0.84248607 0.14631839]
Cela vous indique que 84,2 % de la variance de l’ensemble de données se situe le long du premier axe, et 14,6 % le long du deuxième axe. Il reste donc moins de 1,2 % pour le troisième axe, ce qui permet de supposer qu’il contient probablement peu d’informations.
Choisir le bon nombre de dimensions¶
Au lieu de choisir arbitrairement le nombre de dimensions à réduire, il est généralement préférable de choisir le nombre de dimensions qui représentent une part suffisamment importante de la variance (par exemple 95%). À moins, bien sûr, que vous ne réduisiez la dimensionnalité pour la visualisation des données - dans ce cas, vous voudrez généralement réduire la dimensionnalité à 2 ou 3. Le code suivant calcule l’ACP sans réduire la dimensionnalité, puis calcule le nombre minimum de dimensions nécessaires pour préserver 95% de la variance de l’ensemble de formation :
pca = PCA()
pca.fit(X)
cumsum = np.cumsum(pca.explained_variance_ratio_)
d = np.argmax(cumsum >= 0.95) + 1
Vous pourriez alors définir n_components=d et relancer l’ACP. Cependant, il existe une bien meilleure option : au lieu de spécifier le nombre de composants principaux que vous souhaitez préserver, vous pouvez définir n_components comme un nombre entre 0,0 et 1,0, indiquant le ratio de variance que vous souhaitez préserver :
pca = PCA(n_components=0.95)
X_reduced = pca.fit_transform(X)
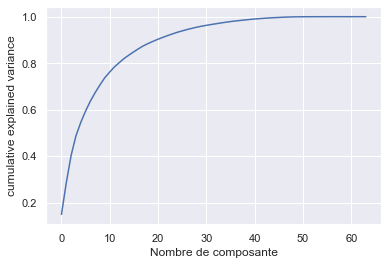
Une autre option encore consiste à tracer la variance expliquée en fonction du nombre de dimensions (simplement tracer cumsum ; voir figure ci-dessous). Il y aura généralement un coude dans la courbe, où la variance expliquée cesse de croître rapidement. Vous pouvez considérer cela comme la dimensionnalité intrinsèque de l’ensemble de données. Dans ce cas, vous pouvez voir que la réduction de la dimensionnalité à environ 100 dimensions ne perdrait pas trop de la variance expliquée.
from sklearn.datasets import load_digits
digits = load_digits()
pca = PCA().fit(digits.data)
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('Nombre de composante')
plt.ylabel('cumulative explained variance');
Réduction de la dimensionnalité par l’ACP¶
L’utilisation de l’ACP pour la réduction de la dimensionnalité implique la mise à zéro d’une ou de plusieurs des plus petites composantes principales, ce qui donne une projection à plus faible dimension des données qui préserve la variance maximale des données.
Voici un exemple d’utilisation de l’ACP comme transformation de réduction de la dimensionnalité :
pca = PCA(n_components=1)
pca.fit(X)
X_pca = pca.transform(X)
print("original shape: ", X.shape)
print("transformed shape:", X_pca.shape)
original shape: (200, 2)
transformed shape: (200, 1)
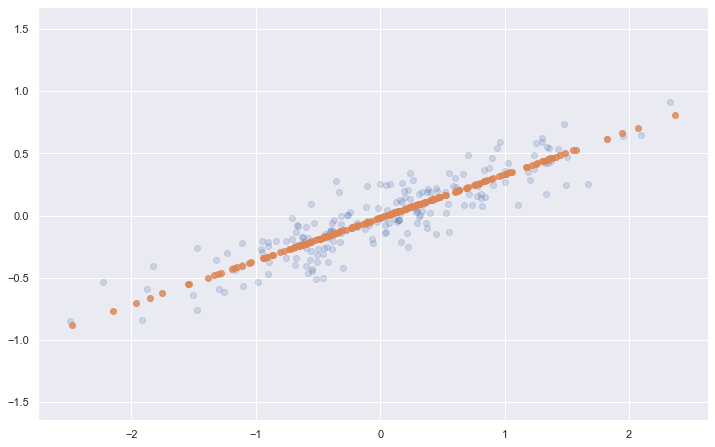
Les données transformées ont été réduites à une seule dimension. Pour comprendre l’effet de cette réduction de dimensionnalité, nous pouvons effectuer la transformation inverse de ces données réduites et la tracer avec les données originales :
fig = plt.figure(figsize=(12, 7.6))
X_new = pca.inverse_transform(X_pca)
plt.scatter(X[:, 0], X[:, 1], alpha=0.2)
plt.scatter(X_new[:, 0], X_new[:, 1], alpha=0.8)
plt.axis('equal');
La régression en composantes principales (PCR)¶
Dans les sections précédentes, nous avons vu que nous avons pu contrôler la variance en réduisant leurs coefficients vers zéro. Avec cette méthode, nous avons utilisé les prédicteurs \(X_{1}, X_{2}, \ldots, X_{p}\). Nous explorons maintenant une classe d’approches qui transforment les prédicteurs et ajustent ensuite un modèle des moindres carrés en utilisant les variables, cette fois, transformées. Nous appellerons ces techniques des méthodes de réduction dimensionnalité.
Soit \(Z_{1}, Z_{2}, \ldots, Z_{M}\) représentent \(M<p\) des combinaisons linéaires de nos prédicteurs \(p\) originaux. C’est-à-dire,
pour certaines constantes \(\phi_{1 m}, \phi_{2 m} \ldots, \phi_{p m}, m=1, \ldots, M .\) Nous pouvons alors ajuster le modèle de régression linéaire
en utilisant les moindres carrés. Notez que dans (6.17), les coefficients de régression sont donnés par. \(\theta_{0}, \theta_{1}, \ldots, \theta_{M}\). Si les constantes \(\theta_{0}, \theta_{1}, \ldots, \theta_{M}\) sont choisies judicieusement, alors ces approches de réduction dimensionnelle peuvent souvent surpasser la régression par moindres carrés. En d’autres termes, l’ajustement (6.17) à l’aide des moindres carrés peut donner de meilleurs résultats que l’ajustement \(Y=\beta_{0}+\beta_{1} X_{1}+\cdots+\beta_{p} X_{p}+\epsilon\) à l’aide des moindres carrés.
Le terme de réduction de la dimension vient du fait que cette approche réduit le problème de l’estimation des \(p+1\) coefficients \(\beta_{0}, \beta_{1}, \ldots, \beta_{p}\) au problème plus simple de l’estimation des \(M+1\) coefficients \(\theta_{0}, \theta_{1}, \ldots, \theta_{M}\), où \(M<p\). En d’autres termes, la dimension du problème a été réduite de \(p+1\) à \(M+1\).
Notez que de (6.16)
où $\( \beta_{j}=\sum_{m=1}^{M} \theta_{m} \phi_{j m} \tag{6.18} \)$
On peut donc considérer (6.17) comme un cas particulier du modèle de régression linéaire originale donné par (6.1). La réduction de la dimension sert à contraindre les coefficients estimés de \(\beta_{j}\), puisqu’ils doivent maintenant prendre la forme (6.18). Cette contrainte sur la forme des coefficients risque de biaiser les estimations des coefficients. Cependant, dans les situations où \(p\) est grand par rapport à \(n\), le choix d’une valeur de \(M \ll p\) peut réduire de manière significative la variance des coefficients ajustés. Si \(M=p\), et que tous les \(Z_{m}\) sont linéairement indépendants, alors (6,18) ne pose aucune contrainte. Dans ce cas, il n’y a pas de réduction de dimension, et l’ajustement (6.17) équivaut donc à effectuer des moindres carrés sur les p prédicteurs originaux.
Toutes les méthodes de réduction des dimensions fonctionnent en deux étapes. Tout d’abord, on obtient les prédicteurs transformés \(Z_{1}, Z_{2}, \ldots, Z_{M}\). Ensuite, le modèle est ajusté à l’aide de ces prédicteurs \(M\). Cependant, le choix de \(Z_{1}, Z_{2}, \ldots, Z_{M},\) ou de manière équivalente, la sélection des \(\phi_{j m}\), peut être réalisé de différentes manières; les composantes principales et les moindres carrés partiels. Dans ce cours, nous étudions la première approche.
Visualization avec l’ACP : Hand-written digits¶
L’utilité de la réduction de la dimensionnalité n’est peut-être pas entièrement apparente dans deux dimensions seulement, mais elle devient beaucoup plus claire lorsqu’on examine des données à haute dimension. Examinons rapidement l’application de l’ACP aux données cHand-written digits
Nous commençons par charger les données :
from sklearn.decomposition import PCA
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shape
(1797, 64)
Rappelons que les données sont constituées d’images de 8×8 pixels, ce qui signifie qu’elles sont en 64 dimensions. Pour avoir une idée des relations entre ces points, nous pouvons utiliser l’ACP pour les projeter sur un nombre plus gérable de dimensions, disons deux :
pca = PCA(2) # project from 64 to 2 dimensions
projected = pca.fit_transform(digits.data)
print(digits.data.shape)
print(projected.shape)
(1797, 64)
(1797, 2)
Nous pouvons maintenant tracer les deux premières composantes principales de chaque point pour en savoir plus sur les données :
fig = plt.figure(figsize=(12, 7.6))
plt.scatter(projected[:, 0], projected[:, 1],
c=digits.target, edgecolor='none', alpha=0.5,
cmap=plt.cm.get_cmap('nipy_spectral', 10))
plt.xlabel('Composante 1')
plt.ylabel('Composante 2')
plt.colorbar();
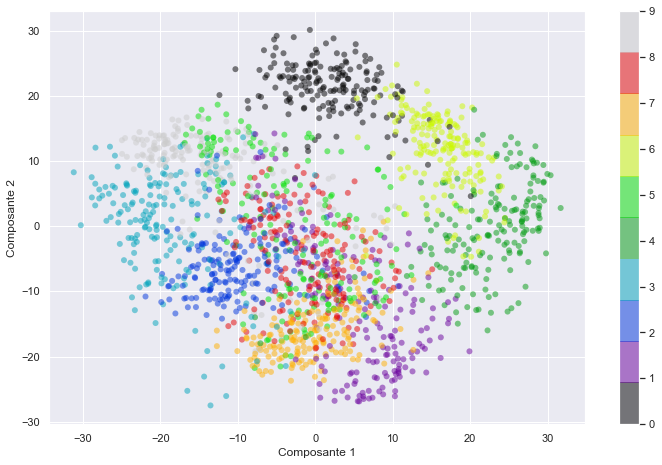
Notons que ces composantes signifient que les données complètes sont un nuage de points en 64 dimensions, et ces points sont la projection de chaque point de données le long des directions ayant la plus grande variance. Nous avons essentiellement trouvé l’étirement et la rotation optimaux dans un espace à 64 dimensions qui nous permet de voir la disposition des chiffres en deux dimensions, et nous l’avons fait de manière non supervisée, c’est-à-dire sans référence aux étiquettes.
L’ACP pour la compression¶
Il est évident qu’après la réduction de la dimensionnalité, la taille de l’ensemble d’entraînement est beaucoup réduite. Par exemple, essayez d’appliquer l’ACP à l’ensemble de données du MNIST tout en préservant 95 % de sa variance. Vous devriez constater que chaque instance aura un peu plus de 150 caractéristiques, au lieu des 784 caractéristiques d’origine. Ainsi, bien que la majeure partie de la variance soit préservée, l’ensemble de données est maintenant inférieur à 20 % de sa taille originale !
C’est un taux de compression raisonnable, et vous pouvez voir comment cela peut accélérer considérablement un algorithme de classification (tel qu’un classificateur SVM).
Il est également possible de décompresser l’ensemble de données réduit à 784 dimensions en appliquant la transformation inverse de la projection PCA. Bien sûr, cela ne vous rendra pas les données originales, puisque la projection a perdu un peu d’information, mais elle sera probablement assez proche des données originales. La distance moyenne au carré entre les données originales et les données reconstruites (compressées puis décompressées) est appelée l’erreur de reconstruction. Par exemple, le code suivant compresse l’ensemble de données MNIST à 154 dimensions, puis utilise la méthode inverse_transform() pour le décompresser à nouveau à 784 dimensions.
La figure ci-dessous montre quelques chiffres de l’ensemble de formation original (à gauche), et les chiffres correspondants après compression et décompression. Vous pouvez voir qu’il y a une légère perte de qualité de l’image, mais les chiffres sont encore pour la plupart intacts.
from sklearn.model_selection import train_test_split
X = mnist["data"]
y = mnist["target"]
X_train, X_test, y_train, y_test = train_test_split(X, y)
pca = PCA()
pca.fit(X_train)
cumsum = np.cumsum(pca.explained_variance_ratio_)
d = np.argmax(cumsum >= 0.95) + 1
d
154
Lorsqu’on fait la transformation
pca = PCA(n_components=0.95)
X_reduced = pca.fit_transform(X_train)
pca.n_components_
154
np.sum(pca.explained_variance_ratio_)
0.9503987558382964
pca = PCA(n_components = 154)
X_reduced = pca.fit_transform(X_train)
X_recovered = pca.inverse_transform(X_reduced)
plt.figure(figsize=(15,8))
plt.subplot(121)
plot_digits(X_train[::2100])
plt.title("Originale", fontsize=16)
plt.subplot(122)
plot_digits(X_recovered[::2100])
plt.title("Compressée", fontsize=16)
Text(0.5, 1.0, 'Compressée')

APC incrémentielle¶
L’un des problèmes de la mise en oeuvre précédente de l’ACP est qu’elle exige que l’ensemble d’entrainement s’inscrive en mémoire pour que l’algorithme de l’SVD (que nous verrons plus tard) puisse fonctionner. Heureusement, des algorithmes PCA incrémentaux (IPCA) ont été développés : vous pouvez diviser l’ensemble d’entrainememt en mini lots et alimenter un algorithme IPCA un mini lot à la fois. Cela est utile pour les grands ensembles d’entraînement, mais aussi pour appliquer l’IPCA en ligne (c’est-à-dire en mode diffusion streaming, à mesure que de nouvelles instances arrivent).
Le code suivant divise l’ensemble de données MNIST en 100 mini lots (à l’aide de la fonction array_split() de NumPy) et les transmet à la classe IPCA incrémentielle5 de Scikit-Learn afin de réduire la dimensionnalité de l’ensemble de données MNIST à 154 dimensions (comme auparavant). Notez que vous devez appeler la méthode partial_fit() avec chaque mini-batch plutôt que la méthode fit() avec l’ensemble de l’entraînement :
from sklearn.decomposition import IncrementalPCA
n_batches = 100
inc_pca = IncrementalPCA(n_components=154)
for X_batch in np.array_split(X_train, n_batches):
print(".", end="") # not shown in the book
inc_pca.partial_fit(X_batch)
X_reduced = inc_pca.transform(X_train)
....................................................................................................
X_recovered_inc_pca = inc_pca.inverse_transform(X_reduced)

Comparons les résultats de la transformation du MNIST en utilisant l’ACP régulière et l’ACP incrémentielle. Tout d’abord, les moyennes sont égales :
np.allclose(pca.mean_, inc_pca.mean_)
True
Mais les résultats ne sont pas exactement identiques. L’ACP incrémentielle donne une très bonne solution approximative, mais elle n’est pas parfaite :
np.allclose(X_reduced_pca, X_reduced_inc_pca)
False
Conclusion¶
Dans cette section, nous avons discuté de l’utilisation de l’analyse par composantes principales pour la réduction de la dimensionnalité, pour la visualisation de données en haute dimension, pour le filtrage du bruit et pour la sélection des caractéristiques dans les données en haute dimension.
En raison de sa polyvalence et de sa capacité d’interprétation, l’ACP s’est avérée efficace dans une grande variété de contextes et de disciplines. Pour tout ensemble de données à haute dimension, nous commençons par l’ACP afin de visualiser la relation entre les points (comme nous l’avons fait avec les chiffres), de comprendre la principale variance des données et de comprendre la dimensionnalité intrinsèque (en traçant le rapport de variance expliqué).
L’ACP n’est certainement pas utile pour tous les ensembles de données à haute dimension, mais elle offre un moyen simple et efficace de comprendre les données à haute dimension.
La principale faiblesse de l’ACP est qu’elle a tendance à être fortement affectée par les valeurs aberrantes des données. C’est pourquoi de nombreuses variantes robustes de l’ACP ont été développées, dont beaucoup agissent de manière itérative en rejetant les points de données qui sont mal décrits par les composantes initiales.
Scikit-Learn contient quelques variantes intéressantes de l’ACP, dont l’ACP Stochastique et l’ACP sparse, toutes deux également dans le sous-module sklearn.decomposition. La méthode RandomizedPCA utilise une méthode non déterministe pour approcher rapidement les premiers composants principaux dans des données à très haute dimension, tandis que SparsePCA introduit un terme de régularisation.
Dans les sections suivantes, nous examinerons d’autres méthodes d’apprentissage non supervisées qui s’appuient sur certaines des idées de l’ACP.
